Chapter 1 - Linear Equations in Linear Algebra

1.9 - The Matrix of a Linear Transformation

Main:	Index
Previous:	1.8 - Introduction to Linear Transformations
Next:	2.1 - Matrix Operations

Results

Theorem 1.10

Let T: ℝⁿ→ℝ^m be a linear transformation. Then there exists a unique matrix A such that $$ T(\bs{x}) = A\bs{x}\qquad \forall\bs{x}\in\R^n. $$ In fact, A is the m×n matrix whose jth column is the vector T(e_j), where e_j is the jth column of the identity matrix in ℝⁿ: $$ A = \big[T(\bs{e}_1) \;\; \cdots \;\;T(\bs{e}_n)\big] $$

Definition: Onto [Surjective]

A mapping $T: \R^n\rightarrow \R^m$ is said to be onto ℝ^m if each b in ℝ^m is the image of at least one x in ℝⁿ.

Definition: One-to-one [Injective]

A mapping $T: \R^n\rightarrow \R^m$ is said to be one-to-one if each b in ℝ^m is the image of at most one x in ℝⁿ.

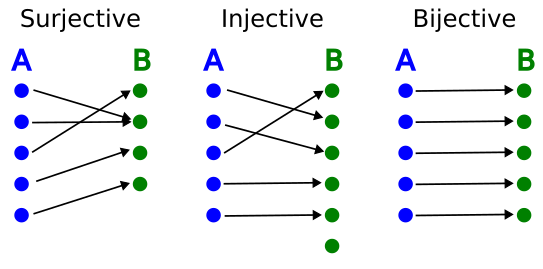
Surjective, or onto, means that every point in B has some A. The set A 'fills' all of B.
Injective, or one-to-one, means that no point in B can mapped to by many points in A.
Bijective means both properties apply at the same time. Perfect pairing between sets.

Theorem 1.11

Let $T: \R^n\rightarrow\R^m$ be a linear transformation. Then T is one-to-one (injective) iff the equation T(x) = 0 has only the trivial solution.

Theorem 1.12

Let $T: \R^n\rightarrow\R^m$ be a linear transformation and let A be the standard matrix for T. Then:
a. T maps ℝⁿ onto ℝ^m iff the columns of A span ℝ^m.
b. T is one-to-one iff the columns of A are linearly independent.

Exercise 2

Let $T: \R^3\rightarrow\R^2$, T(e₁) = (1, 3), T(e₂) = (4, -7) and T(e₃) = (-5, 4) where e_i are the vectors of the identity matrix. Find the standard matrix of T.

Answer
By Theorem 1.10, we have: $$ A = \big[T(\bs{e}_1) \;\; T(\bs{e}_2) \;\;T(\bs{e}_3)\big] = \begin{bmatrix*}[rrr] 1 & 4 & -5 \\ 3 & -7 & 4 \end{bmatrix*} $$

■

Exercise 10

T: ℝ²→ℝ² first reflects points through the vertical x₂-axis and then rotates points by $\pi/2$ radians. Find the standard matrix of T.

Answer
The matrix for reflecting over the x₂-axis (or y-axis) is given as: $$ A_1 = \begin{bmatrix*}[rr] -1 & 0 \\ 0 & 1 \end{bmatrix*} $$ The matrix for rotating points by a certain degree $\phi$: $$ A_2 = \begin{bmatrix*}[rr] \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{bmatrix*} $$ Multiplying them together gives us the matrix: $$ A = A_1A_2 = \begin{bmatrix*}[rr] -\cos\phi & -\sin\phi \\ -\sin\phi & \cos\phi \end{bmatrix*} $$ Putting in $\phi = \pi/2$. $$ A = \begin{bmatrix*}[rr] -\cos\pi/2 & -\sin\pi/2 \\ -\sin\pi/2 & \cos\pi/2 \end{bmatrix*} = \begin{bmatrix*}[rr] 0 & -1 \\ -1 & 0 \end{bmatrix*} $$ This is the same as reflection through the line $x_2 = -x_1$.

■

Exercise 19

Show that T is a linear transformation by finding a matrix that implements the mapping. $$ T(x_1,x_2,x_3) = (x_1 - 5x_2 + 4x_3, x_2 - 6x_3) $$

Answer
Requires a 3×1 input vector, and outputs a 2×1 vector, so the matrix will be a 2×3 matrix. The first row will be: (1, -5, 4) and the second row will be (0, 1, -6). So: $$ A = \begin{bmatrix*}[rrr] 1 & -5 & 4 \\ 0 & 1 & -6 \end{bmatrix*} $$ Verifying: $$ \begin{bmatrix*}[rrr] 1 & -5 & 4 \\ 0 & 1 & -6 \end{bmatrix*} \begin{bmatrix*}[r] x_1 \\ x_2 \\ x_3 \end{bmatrix*} = \begin{bmatrix*}[rcrcr] (1)(x_1) &+& (-5)(x_2) &+& (4)(x_3) \\ (0)(x_1) &+& (1)(x_2) &+& (-6)(x_3) \end{bmatrix*} = \begin{bmatrix*}[r] x_1 - 5x_2 + 4x_3\\ x_2 - 6x_3 \end{bmatrix*} = T(x_1,x_2,x_3) $$

■

Exercise 23

Verifying statements. Answer True or False and justify the answer.

(a) A linear transformation T: ℝⁿ→ℝ^m is completely determined by its effect on the columns of the n×n identity matrix.
Answer: True. This is verified in Theorem 1.10.

(b) If T: ℝ²→ℝ² rotates vectors about the origin by an angle $\phi$, then T is a linear transformation.
Answer: True. The standard matrix is: $$ A = \begin{bmatrix*}[rr] \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{bmatrix*} $$

(c) When two linear transformations are performed one after the another, the combined effect may not always be a linear transformation.
Answer: False. Every linear transformation is a matrix. When doing two of them this will simply correspond to multiplying the matrices.

(d) A mapping T: ℝⁿ→ℝ^m is onto (surjective) ℝ^m if every vector x in ℝⁿ maps onto some vector in ℝ^m.
Answer: False. It would be onto if every vector in ℝ^m has some associated vector in ℝⁿ.

(e) If A is a 3×2 matrix, then the transformation x→Ax cannot be one-to-one.
Answer: False. The associated linear transformation would be T: ℝ²→ℝ³. The one-to-one (injective) mapping means that any point in ℝ³ has at most one associated point in ℝ². If we define: $$ A = \begin{bmatrix*}[rr] 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{bmatrix*} $$ then for some point (x₁, x₂): $$ \begin{bmatrix*}[rr] 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{bmatrix*}\begin{bmatrix*}[r] x_1 \\ x_2 \end{bmatrix*} = \begin{bmatrix*}[rr] x_1 \\ x_2 \\ 0 \end{bmatrix*} $$ In this case we have constructed a one-to-one mapping, though only to a plane in ℝ³.

■

Exercise 24

Verifying statements. Answer True or False and justify the answer.

(a) Not every linear transformation from ℝⁿ to ℝ^m is a matrix transformation.
Answer: False. Not every linear transformation is a matrix transformation, but every linear transformation between ℝⁿ and ℝ^m are. (See text after Theorem 1.10 in the text book).

(b) The columns of the standard matrix for a linear transformation from ℝⁿ to ℝ^m are the images of the columns of the n×n matrix.
Answer: True. This is the statement from Theorem 1.10.

(c) The standard matrix of a linear transformation from ℝ² to ℝ² that reflects points through the horizontal axis, the vertical axis, or the origin has the form: $$ \begin{bmatrix*}[rr] a & 0 \\ 0 & d \end{bmatrix*}, $$ where a and d are +/-1.
Answer: True. Check reflection matrices on page 101.

(d) A mapping T: ℝⁿ → ℝ^m is one-to-one if each vector in ℝⁿ maps to a unique vector in ℝ^m.
Answer: False. The injective property only says that no two points in ℝⁿ can map to the same point in ℝ^m. It does not say that it has to for each point in the domain.

(e) If A is a 3×2 matrix, then the transformation x→Ax cannot map ℝ² to ℝ³.
Answer: True, assuming that we mean the entire space. Since ℝ³ is a bigger space, we can never find an associated point in ℝ² for every point in ℝ³.

■

Exercise 35

If a linear transformation T: ℝⁿ→ ℝ^m maps ℝⁿ onto ℝ^m, can you give a relation between m and n? If T is one-to-one, what can you say about m and n?

Answer
Assuming we mean filling the entire space. In order for a mapping to be 'onto' or surjective, it has to fill the entire codomain. This is only possible if the domain is larger than the codomain. In other words: n ≥ m.

If T is one-to-one, each point in the codomain has at most one point in the domain. In other words: n ≤ m.

■