Chapter 1 - Linear Equations in Linear Algebra

1.8 - Introduction to Linear Transformations

Main:	Index
Previous:	1.7 - Linear Independence
Next:	1.9 - The Matrix of a Linear Transformation

Results

The difference between a matrix equation Ax = b and the associated vector equation $$ x_1\bs{a}_1 + \cdots + x_n\bs{a}_n = \bs{b} $$ is merely a matter of notation. However, a matrix equation can arise in linear algebra in a way that is not directly connected with linear combination of vectors. In this case we think of the matrix A as an object that acts on a vector x by multiplication to produce a new vector called Ax.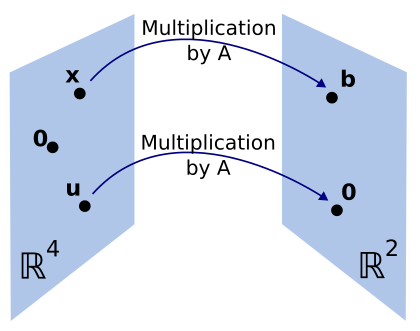



From this perspective, solving the equation Ax = b amounts to finding all vectors x in ℝ⁴ that are transformed into the vector b in ℝ² under the "action" of multiplication by A. (Similar to note made earlier).

This correspondence from x to Ax is a function from one set of vectors to another. A transformation (or function or mapping) T from ℝⁿ to ℝ^m is a rule that assigns to each vector x in ℝⁿ a vector T(x) in ℝ^m. The set ℝⁿ is called the domain of T, and ℝ^m is called the codomain of T.

Matrix Transformations

In the rest of this section T(x) is computed as Ax, where A is an m×n matrix.

Example
Given the following: $$ A = \begin{bmatrix*}[rr] 1 & -3 \\ 3 & 5 \\ -1 & 7 \end{bmatrix*},\quad \bs{u} = \begin{bmatrix*}[r] 2 \\ -1 \end{bmatrix*},\quad \bs{b} = \begin{bmatrix*}[r] 3 \\ 2 \\ -5 \end{bmatrix*},\quad \bs{c} = \begin{bmatrix*}[r] 3 \\ 2 \\ 5 \end{bmatrix*} $$ and define the transformation T: ℝ² → ℝ³ by T(x) = Ax.

(a) Find T(u), the image under u under the transformation T.
(b) Find an x in ℝ² whose image under T is b.
(c) Is there more than one x whose image under T is b?
(d) Determine if c is in the range of the transformation T.


Solutions

(a)
Compute: $$ T(\bs{u}) = A\bs{u} = \begin{bmatrix*}[rr] 1 & -3 \\ 3 & 5 \\ -1 & 7 \end{bmatrix*} \begin{bmatrix*}[r] 2 \\ -1 \end{bmatrix*} = \begin{bmatrix*}[r] 2 + 3 \\ 6 - 5 \\ -2 - 7 \end{bmatrix*} = \begin{bmatrix*}[r] 5 \\ 1 \\ -9 \end{bmatrix*} $$

(b)
Solve T(x) = b for x, or solve Ax = b: $$ \begin{bmatrix*}[rr] 1 & -3 \\ 3 & 5 \\ -1 & 7 \end{bmatrix*} \begin{bmatrix*}[r] x_1 \\ x_2 \end{bmatrix*} = \begin{bmatrix*}[r] 3 \\ 2 \\ -5 \end{bmatrix*} $$ Writing the augmented matrix and solving: $$ \begin{bmatrix*}[rr] 1 & -3 & 3\\ 3 & 5 & 2\\ -1 & 7 & -5 \end{bmatrix*} \sim \begin{bmatrix*}[rrr] 1 & 0 & 1.5 \\ 0 & 1 & -0.5 \\ 0 & 0 & 0 \end{bmatrix*} $$ Hence the solution is $x_1 = 1.5$ and $x_2 = -0.5$.

(c)
From (b) we can see that there is a unique solution, so there is only one x that maps to the vector b.

(d)
The vector c is in range of T if c is the image of some x in ℝ². That is, if c = T(x) for some x. This is another way of asking if Ax = c is consistent. Checking the augmented matrix: $$ \begin{bmatrix*}[rrr] 1 & -3 & 3 \\ 3 & 5 & 2 \\ -1 & 7 & 5 \end{bmatrix*} \sim \begin{bmatrix*}[rrr] 1 & -3 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & -35 \end{bmatrix*} $$ This system is inconsistent, so c is not in the range of T.

Linear Transformations

Theorem 1.5 shows that an m×n matrix has the properties $$ A(\bs{u} + \bs{v}) = A\bs{u} + A\bs{v} \quad\text{and}\quad A(c\bs{u}) = cA\bs{u} $$ for all $\bs{u}, \bs{v}\in\R^n$ and all scalars $c\in\R$. These properties, written in function notation, identify the most important class of transformations in linear algebra.



Every matrix transformation is a linear transformation, and they preserve the operation of vector addition and scalar multiplication. Some immediate facts that follows from the definition:

Exercise 1

Let $$ A = \begin{bmatrix*}[rr] 2 & 0 \\ 0 & 2 \end{bmatrix*}, $$ and define $T: \R^2 \rightarrow \R^2$ by $T(\bs{x}) = A\bs{x}$. Find the images under T of u = (1, -3) and v = (a, b).

Answer
$$ T(\bs{u}) = A\bs{u} = \begin{bmatrix*}[rr] 2 & 0 \\ 0 & 2 \end{bmatrix*} \begin{bmatrix*}[r] 1 \\ -3 \end{bmatrix*} = \begin{bmatrix*}[c] 2(1) + 0(-3) \\ 0(1) + 2(-3) \end{bmatrix*} = \begin{bmatrix*}[c] 2 + 0 \\ 0 - 6 \end{bmatrix*} = \begin{bmatrix*}[r] 2 \\ -6 \end{bmatrix*} $$ $$ T(\bs{v}) = A\bs{v} = \begin{bmatrix*}[rr] 2 & 0 \\ 0 & 2 \end{bmatrix*} \begin{bmatrix*}[r] a \\ b \end{bmatrix*} = \begin{bmatrix*}[r] 2a \\ 2b \end{bmatrix*} $$

Exercise 5

With T defined as $T(\bs{x}) = A\bs{x}$, find a vector x whose image under T is b and determine whether x is unique. $$ A = \begin{bmatrix*}[rrr] 1 & -5 & -7 \\ -3 & 7 & 5 \end{bmatrix*}, \bs{b} = \begin{bmatrix*}[r] -2 \\ -2 \end{bmatrix*} $$

Answer
So, we need to find an x so Ax = b. Writing out the augmented matrix. We already see that there are more vectors than entries, so we will have a linear dependence between the coefficient columns and therefore not a unique solution. $$ \begin{bmatrix*}[rrrr] 1 & -5 & -7 & -2 \\ -3 & 7 & 5 & -2 \end{bmatrix*} $$ II + 3I $$ \begin{bmatrix*}[rrrr] 1 & -5 & -7 & -2 \\ 0 & -8 & -16 & -8 \end{bmatrix*} $$ (-1/8)II $$ \begin{bmatrix*}[rrrr] 1 & -5 & -7 & -2 \\ 0 & 1 & 2 & 1 \end{bmatrix*} $$ I + 5II $$ \begin{bmatrix*}[rrrr] 1 & 0 & 3 & 3 \\ 0 & 1 & 2 & 1 \end{bmatrix*} $$ Solution set: $$ \left\{ \begin{array}{l} x_1 = 3 - 3x_3 \\ x_2 = 1 - 2x_3 \\ x_3 \text{ free} \end{array} \right. $$ Fixing $x_3 = 0$ so $x_1 = 3$ and $x_2 = 1$ and verifying: $$ \begin{bmatrix*}[rrr] 1 & -5 & -7\\ -3 & 7 & 5 \end{bmatrix*} \begin{bmatrix*}[r] 3 \\ 1 \\ 0 \end{bmatrix*} \;=\; \begin{bmatrix*}[rcrcr] 1(3) &+& (-5)(1) &+& (-7)(0) \\ (-3)(3) &+& 7(1) &+& 5(0) \end{bmatrix*} \;=\; \begin{bmatrix*}[c] 3 - 5 + 0 \\ -9 + 7 + 0 \end{bmatrix*} \;=\; \begin{bmatrix*}[c] -2 \\ -2 \end{bmatrix*} $$ And just to verify that the solution is not unique, set $x_3 = 1$ which gives $x_1 = 0$ and $x_2 = -1$. $$ \begin{bmatrix*}[rrr] 1 & -5 & -7\\ -3 & 7 & 5 \end{bmatrix*} \begin{bmatrix*}[r] 0 \\ -1 \\ 1 \end{bmatrix*} \;=\; \begin{bmatrix*}[rcrcr] 1(0) &+& (-5)(-1) &+& (-7)(1) \\ (-3)(0) &+& 7(-1) &+& 5(1) \end{bmatrix*} \;=\; \begin{bmatrix*}[c] 0 + 5 - 7 \\ 0 - 7 + 5 \end{bmatrix*} \;=\; \begin{bmatrix*}[c] -2 \\ -2 \end{bmatrix*} $$

Exercise 9

Find all x in ℝ⁴ that are mapped into the zero vector by the transformation b → Ax for the matrix A: $$ A = \begin{bmatrix*}[rrrr] 1 & -4 & 7 & -5 \\ 0 & 1 & -4 & 3 \\ 2 & -6 & 6 & -4 \end{bmatrix*} $$

Answer
So, find all vectors x such that Ax = 0. Defining the augmented matrix with the zero vector. $$ \begin{bmatrix*}[rrrrr] 1 & -4 & 7 & -5 & 0 \\ 0 & 1 & -4 & 3 & 0 \\ 2 & -6 & 6 & -4 & 0 \end{bmatrix*} $$ III - 2I $$ \begin{bmatrix*}[rrrrr] 1 & -4 & 7 & -5 & 0 \\ 0 & 1 & -4 & 3 & 0 \\ 0 & 2 & -8 & 6 & 0 \end{bmatrix*} $$ (1/2)III $$ \begin{bmatrix*}[rrrrr] 1 & -4 & 7 & -5 & 0 \\ 0 & 1 & -4 & 3 & 0 \\ 0 & 1 & -4 & 3 & 0 \end{bmatrix*} $$ III - 2II $$ \begin{bmatrix*}[rrrrr] 1 & -4 & 7 & -5 & 0 \\ 0 & 1 & -4 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix*} $$ No pivot column in the third row - so there are at keast two free variables. We can see that there are pivot columns in rows 1 and 2, so there are two variables and two free variables. I + 4II $$ \begin{bmatrix*}[rrrrr] 1 & 0 & -9 & 7 & 0 \\ 0 & 1 & -4 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix*} $$ Solution set: $$ \left\{ \begin{array}{l} x_1 = 9x_3 - 7x_4 \\ x_2 = 4x_3 - 3x_3 \\ x_3 \text{ free} \\ x_4 \text{ free} \end{array} \right. $$ Verifying: setting $x_3 = x_4 = 1$ so $x_1 = 2$ and $x_2 = 1$. Checking that this gives the 0 vector: $$ \begin{bmatrix*}[rrrr] 1 & -4 & 7 & -5 \\ 0 & 1 & -4 & 3 \\ 2 & -6 & 6 & -4 \end{bmatrix*} \begin{bmatrix*}[r] 2 \\ 1 \\ 1 \\ 1 \end{bmatrix*} = \begin{bmatrix*}[rcrcrcr] 1(2) &+& (-4)(1) &+& 7(1) &+& (-5)(1) \\ 0(2) &+& 1(1) &+& (-4)(1) &+& 3(1) \\ 2(2) &+& (-6)(1) &+& 6(1) &+& (-4)(1) \end{bmatrix*} = \begin{bmatrix*}[c] 2 - 4 + 7 - 5 \\ 0 + 1 - 4 + 3 \\ 4 - 6 + 6 - 4 \end{bmatrix*} = \begin{bmatrix*}[c] 0 \\ 0 \\ 0 \end{bmatrix*} $$

Exercise 11

Using the matrix from exercise 9. Check if b = (-1, 1, 0) is in the range of the linear transformation x→Ax.

Answer
Writing the augmented matrix with b instead of the zero vector. We just repeat the row operations and check if we get a contradiction. $$ \begin{bmatrix*}[rrrrr] 1 & -4 & 7 & -5 & -1 \\ 0 & 1 & -4 & 3 & 1 \\ 2 & -6 & 6 & -4 & 0 \end{bmatrix*} $$ III - 2I $$ \begin{bmatrix*}[rrrrr] 1 & -4 & 7 & -5 & -1 \\ 0 & 1 & -4 & 3 & 1 \\ 0 & 2 & -8 & 6 & 2 \end{bmatrix*} $$ (1/2)III $$ \begin{bmatrix*}[rrrrr] 1 & -4 & 7 & -5 & -1 \\ 0 & 1 & -4 & 3 & 1 \\ 0 & 1 & -4 & 3 & 1 \end{bmatrix*} $$ III - 2II $$ \begin{bmatrix*}[rrrrr] 1 & -4 & 7 & -5 & -1 \\ 0 & 1 & -4 & 3 & 1 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix*} $$ I + 4II $$ \begin{bmatrix*}[rrrrr] 1 & 0 & -9 & 7 & 3 \\ 0 & 1 & -4 & 3 & 1 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix*} $$ This shows that b is in the range of Ax and it has an infinite amount of solutions. The solution set: $$ \left\{ \begin{array}{l} x_1 = 3 + 9x_3 - 7x_4 \\ x_2 = 1 + 4x_3 - 3x_3 \\ x_3 \text{ free} \\ x_4 \text{ free} \end{array} \right. $$ Verifying: setting $x_3 = x_4 = 0$ so $x_1 = 3$ and $x_2 = 1$. Checking: $$ \begin{bmatrix*}[rrrr] 1 & -4 & 7 & -5 \\ 0 & 1 & -4 & 3 \\ 2 & -6 & 6 & -4 \end{bmatrix*} \begin{bmatrix*}[r] 3 \\ 1 \\ 0 \\ 0 \end{bmatrix*} = \begin{bmatrix*}[rcrcrcr] 1(3) &+& (-4)(1) &+& 7(0) &+& (-5)(0) \\ 0(3) &+& 1(1) &+& (-4)(0) &+& 3(0) \\ 2(3) &+& (-6)(1) &+& 6(0) &+& (-4)(0) \end{bmatrix*} = \begin{bmatrix*}[r] 3 - 4 + 0 \\ 0 + 1 + 0 \\ 6 - 6 + 0 \end{bmatrix*} = \begin{bmatrix*}[r] -1 \\ 1 \\ 0 \end{bmatrix*} $$

Exercise 19

Let: $$ \bs{e}_1 = \begin{bmatrix*}[r] 1 \\ 0 \end{bmatrix*},\quad \bs{e}_2 = \begin{bmatrix*}[r] 0 \\ 1 \end{bmatrix*},\quad \bs{y}_1 = \begin{bmatrix*}[r] 2 \\ 5 \end{bmatrix*},\quad \bs{y}_2 = \begin{bmatrix*}[r] -1 \\ 6 \end{bmatrix*} $$ Let T: ℝ² →ℝ² be a linear transformation that maps e₁ to y₁ and e₂ to y₂. Find the images of (5, -3) and (x₁, x₂).

Answer
We can see that the columns of the matrix A associated with the linear mapping is given in the y vectors. Then: $$ A = \begin{bmatrix*}[rr] 2 & -1 \\ 5 & 6 \end{bmatrix*} $$ For instance: $$ A\bs{e}_1 = \begin{bmatrix*}[rr] 2 & -1 \\ 5 & 6 \end{bmatrix*} \begin{bmatrix*}[r] 1 \\ 0 \end{bmatrix*} = \begin{bmatrix*}[r] 2 \\ 5 \end{bmatrix*} $$ First image: $$ \begin{bmatrix*}[rr] 2 & -1 \\ 5 & 6 \end{bmatrix*} \begin{bmatrix*}[r] 5 \\ -3 \end{bmatrix*} = \begin{bmatrix*}[rcr] 2(5) &+& (-1)(-3) \\ 5(5) &+& 6(-3) \end{bmatrix*} = \begin{bmatrix*}[c] 10 + 3 \\ 25 - 18 \end{bmatrix*} = \begin{bmatrix*}[r] 13 \\ 7 \end{bmatrix*} $$ First image: $$ \begin{bmatrix*}[rr] 2 & -1 \\ 5 & 6 \end{bmatrix*} \begin{bmatrix*}[r] x_1 \\ x_2 \end{bmatrix*} = \begin{bmatrix*}[rcr] 2(x_1) &+& (-1)(x_2) \\ 5(x_1) &+& 6(x_2) \end{bmatrix*} = \begin{bmatrix*}[c] 2x_1 - x_2 \\ 5x_1 + 6x_2 \end{bmatrix*} $$

Exercise 21

Verifying statements. Answer True or False and justify the answer.

(a) A linear transformation is a special type of function.
Answer: True. It is a function that satisfies the definition mentioned earlier.

(b) If A is a 3×5 matrix and t is a transformation defined by T(x) = Ax, then the domain of T is ℝ³.
Answer: False. The input to A is a vector with dimensions 5×1 and outputs a vector of 3×1. So the domain is ℝ⁵ and the codomain is ℝ³.

(c) If A is an m×n matrix, then the range of the transformation x→Ax is ℝ^m.
Answer: True. The range and codomain are the same thing, and as in (b) they correspond with the number of rows of the matrix. In this case, they coincide.

(d) Every linear transformation is a matrix transformation.
Answer: False. There are linear transformations that are not matrix transformations (and as the text says they will be covered in chapters 4 and 5).

(e) A transformation T is linear iff $$ T(c_1\bs{v}_1 + c_2\bs{v}_2) = c_1T(\bs{v}_1) + c_2T(\bs{v}_2) $$ for all $\bs{v}_i$ in the domain of T for for all scalars $c_i$.
Answer: True. This is the precise definition of linear transformations.

Exercise 22

Verifying statements. Answer True or False and justify the answer.

(a) Every matrix transformation is a linear transformation.
Answer: True. Follows from Theorem 1.5.

(b) The codomain of the transformation x→Ax is the set of all linear combinations of the columns of A.
Answer: True. Follows from the definition of how matrices are multiplied by vectors.

(c) If T: ℝⁿ→ℝ^m is a linear transformation and if c is in ℝ^m, then a uniqueness question is: "Is c in the range of T?".
Answer: False. If c was in the range a uniqueness question would be if it had a unique vector x in the domain.

(d) A linear transformation preserves the operations of vector addition and scalar multiplication.
Answer: True. This follows from the definition.

(e) The superposition principle is a physical description of a linear transformation.
Answer: True. Particularly the more general statement for n terms.

Exercise 26

Let u and v be linearly independent vectors in ℝ³, and let P be the plane through u, v, and 0. The parametric equation of P is $$ \bs{x} = s\bs{u} + t\bs{v},\qquad s,t\in\R. $$ Show that the linear transformation T: ℝ³→ ℝ³ maps P onto a plane through 0, or onto a line through 0, or onto the just the origin of ℝ³. What must be true of T(u) and T(v) in order for the image of the plane P to be a plane?

Answer
If s, t can be any variable, we will get a 2D plane in ℝ³. If we fix s=0, we are left with $$ \bs{x} = t\bs{v},\qquad t\in\R. $$ which forms a line through the origin (same is true if we fix t = 0). And finally, if both s=t=0 are fixed, we get x = 0, and we map all values to the origin.

Writing out the linear operation: $$ T(\bs{u}) + T(\bs{v}) = T(\bs{u} + \bs{v}) = A(\bs{u} + \bs{v}). $$ In order to preserve the mapping to a plane, one of the columns in A must be the 0 vector.

Exercise 29

Define f: ℝ→ℝ by $f(x) = mx + b$.
(a) Show that f is a linear transformation when b = 0.
(b) Find a property of a linear transformation that is violated when b≠0.
(c) Why is f called a linear transformation?

Answer


(a) Assuming that b = 0 and inputing variables w and y. Then: $$ f(w) + f(y) = mw + 0 + my + 0 = mw + my $$ $$ f(w + y) = m(w + y) + 0 = mw + my $$ So $f(w) + f(y) = f(w + y)$. This shows the first property of linear transformations is satisfied. For some c in ℝ: $$ cf(w) = c(mw + 0) = cmw. $$ $$ f(cw) = m(cw) + 0 = cmw. $$ So $cf(w) = f(cw)$ which verifies the second property of linear transformations.

(b) If b≠0, then the second property is violated. Let's say b = 2 and c = 2. $$ f(2w) = m(2w) + 2 = 2mw + 2 $$ $$ 2f(w) = 2(mw + 2) = 2mw + 4 $$ Now $f(2w)\not=2f(w)$.

(c) A common misconception is to name the functions after the straight lines we get, but the true term refers to the linearity of the operations. We can have linear functions which are not straight lines or straight planes.

Exercise 30

An affine transformation T: ℝⁿ→ℝ^m has the form Ax + b, with A an m×n matrix and b in ℝ^m. Show that T is not a linear transformation when b≠0.

Answer
This is compeltely analogous to part (b) of the previous exercise. Let's set c = 2, then the second property will be violated. $$ T(2\bs{x}) = A(2\bs{x}) + \bs{b} = 2A\bs{x} + \bs{b} $$ $$ 2T(\bs{x}) = 2(A\bs{x} + \bs{b}) = 2A\bs{x} + 2\bs{b}. $$ Now $T(2\bs{x}) \not= 2T(\bs{x})$ if b≠0.