\( \def\R{\mathbb{R}} \def\N{\mathbb{N}} \def\Z{\mathbb{Z}} \def\Q{\mathbb{Q}} \def\eps{\varepsilon} \def\epsilon{\varepsilon} \newcommand\bs[1]{\boldsymbol{#1}} \renewcommand{\geq}{\geqslant} \renewcommand{\leq}{\leqslant} \)

Chapter 1 - Linear Equations in Linear Algebra

1.3 - Vector Equations


Main: Index
Previous: 1.2 - Row Reduction and Echelon Forms
Next: 1.4 - The matrix equation Ax = b


Results

Vectors

Properties of linear systems can be described using concepts and notations of vectors. A matrix with one row is called a column vector or just a vector. Examples of vectors: $$ \bs{u} = \begin{bmatrix*}[r] 3 \\ -1 \end{bmatrix*}, \quad \bs{v} = \begin{bmatrix*}[r] .2 \\ .3 \end{bmatrix*}, \quad \bs{w} = \begin{bmatrix*}[r] w_1 \\ w_2 \end{bmatrix*} $$ The space of all 2-element vectors is denoted by $\R^2$.

Adding and scaling vectors: $$ \begin{bmatrix*}[r] 1 \\ -2 \end{bmatrix*} + \begin{bmatrix*}[r] 2 \\ 5 \end{bmatrix*} = \begin{bmatrix*}[r] 1 + 2 \\ -2 + 5 \end{bmatrix*} = \begin{bmatrix*}[r] 3 \\ 3 \end{bmatrix*} $$ $$ c = 5,\quad\bs{u} = \begin{bmatrix*}[r] 3 \\ -1 \end{bmatrix*} \quad\text{then}\quad c\bs{u} = 5 \begin{bmatrix*}[r] 3 \\ -1 \end{bmatrix*} = \begin{bmatrix*}[r] 15 \\ -5 \end{bmatrix*} $$ In this case we call c a scalar.

Vectors can be visualized by drawing an arrow from the origin to the point. For instance, for vectors: $$ \begin{bmatrix*}[r] 2 \\ 2 \end{bmatrix*},\quad \begin{bmatrix*}[r] -2 \\ -1 \end{bmatrix*},\quad \begin{bmatrix*}[r] 3 \\ -1 \end{bmatrix*} $$ we get:



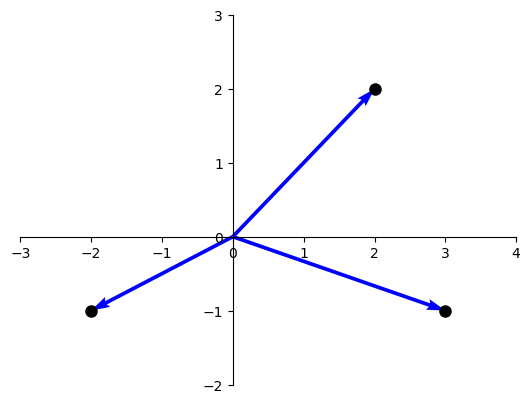
Vectors work in the same way in $\R^3$ and more generally to $\R^n$. $$ \bs{a} = \begin{bmatrix*}[r] 2 \\ 3 \\ 4 \end{bmatrix*},\quad \bs{u} = \begin{bmatrix*}[r] u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix*} $$

Algebraic Properties of $\R^n$


Linear Combinations

For vectors $\bs{v}_1, \ldots, \bs{v}_p$ in $\R^n$ and scalars $c_1,\ldots,c_p$, the vector defined by: $$ \bs{y} = c_1\bs{v}_1 + \ldots + c_p\bs{v}_p $$ is called a linear combination of the vectors with the scalars called weights.



Example

Given the vectors: $$ \bs{a_1} = \begin{bmatrix*}[r] 1 \\ -2 \\ -5 \end{bmatrix*},\quad \bs{a_2} = \begin{bmatrix*}[r] 2 \\ 5 \\ 6 \end{bmatrix*},\quad \bs{b} = \begin{bmatrix*}[r] 7 \\ 4 \\ -3 \end{bmatrix*}. $$ Can we write b as a linear combination of the two other vectors? In other words, can we find weights $x_1, x_2$ such that: $$ x_1\bs{a}_1 + x_2\bs{a}_2 = \bs{b}. $$ By replacing in the vectors, we can write this as: $$ x_1 \begin{bmatrix*}[r] 1 \\ -2 \\ -5 \end{bmatrix*} + x_2 \begin{bmatrix*}[r] 2 \\ 5 \\ 6 \end{bmatrix*} = \begin{bmatrix*}[r] 7 \\ 4 \\ -3 \end{bmatrix*} $$ Which can be written as: $$ \begin{bmatrix*}[r] x_1 \\ -2x_1 \\ -5x_1 \end{bmatrix*} + \begin{bmatrix*}[r] 2x_2 \\ 5x_2 \\ 6x_2 \end{bmatrix*} = \begin{bmatrix*}[r] 7 \\ 4 \\ -3 \end{bmatrix*} $$ $$ \begin{bmatrix*}[r] x_1 + 2x_2 \\ -2x_1 + 5x_2 \\ -5x_1 + 6x_2 \end{bmatrix*} = \begin{bmatrix*}[r] 7 \\ 4 \\ -3 \end{bmatrix*} $$ Which in turn can be represented as the linear system: $$ \begin{array}{rcccr} x_1 & + & 2x_2 & = & 7 \\ -2x_1 & + & 5x_2 & = & 4 \\ -5x_1 & + & 6x_2 & = & -3 \end{array} $$ The problem essentially becomes solving this system for $x_i$. We write the augmented matrix and find RREF. $$ \begin{bmatrix*}[rrr] 1 & 2 & 7 \\ -2 & 5 & 4 \\ -5 & 6 & -3 \end{bmatrix*} \sim \begin{bmatrix*}[rrr] 1 & 0 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{bmatrix*} $$ This has a solution, so b is a linear combination of the vectors. Verifying: $$ 3 \begin{bmatrix*}[r] 1 \\ -2 \\ -5 \end{bmatrix*} + 2 \begin{bmatrix*}[r] 2 \\ 5 \\ 6 \end{bmatrix*} \;=\; \begin{bmatrix*}[r] 3 \\ -6 \\ -15 \end{bmatrix*} + \begin{bmatrix*}[r] 4 \\ 10 \\ 12 \end{bmatrix*} \;=\; \begin{bmatrix*}[r] 7 \\ 4 \\ -3 \end{bmatrix*} $$ Note: to highlight the columns as vectors, we can represent the augmented matrix as: $$ [\bs{a}_1\quad \bs{a}_2\quad \bs{b}] $$

This can be summarized as follows. A vector equation $$ x_1\bs{a}_1 + x_2\bs{a}_2 + \ldots + x_n\bs{a}_n = \bs{b} $$ has the same solution set as the linear system whose augmented matrix is: $$ [\bs{a}_1\quad \bs{a}_2\quad \cdots \quad \bs{a}_n\quad \bs{b}] $$

Definition: span
If $\bs{v}_1, \ldots, \bs{v}_p$ are in $\R^n$, then the set of all linear combinations of $\bs{v}_1, \ldots, \bs{v}_p$ is denoted by Span$\{\bs{v}_1, \ldots, \bs{v}_p\}$ and is called the subset of $\R^n$ spanned or generated by $\bs{v}_1, \ldots, \bs{v}_p$. It is the colletion of all vectors that can be written on the form $$ c_1\bs{v}_1 + \ldots c_p\bs{v}_p $$ where $c_i$ are scalars.


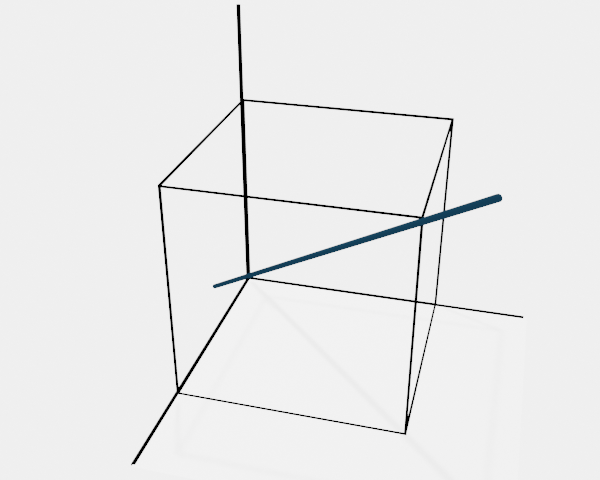
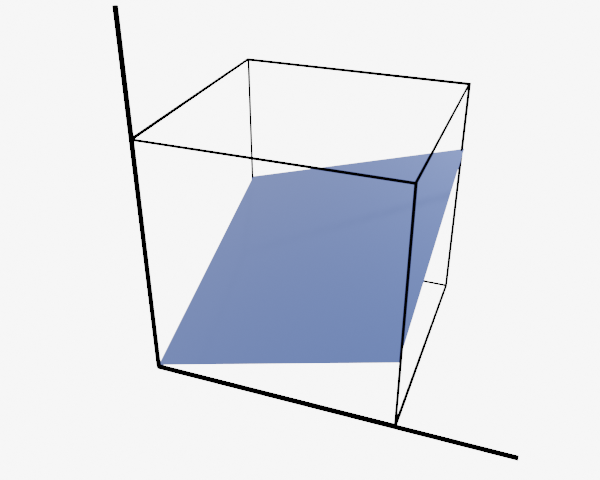
Illustration of Span$\{\bs{v}_1\}$ and Span$\{\bs{v}_1, \bs{v}_2\}$.







Practice Problem

Prove that $\bs{u} + \bs{v} = \bs{v} + \bs{u}$ for any $\bs{u}, \bs{v}$ in $\R^4$.

Answer
$$ \bs{u} + \bs{v} = \begin{bmatrix*}[c] u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix*} + \begin{bmatrix*}[c] v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix*} = \begin{bmatrix*}[c] u_1 + v_1 \\ u_2 + v_2 \\ \vdots \\ u_n + v_n \end{bmatrix*} = \begin{bmatrix*}[c] v_1 + u_1 \\ v_2 + u_2 \\ \vdots \\ v_n + u_n \end{bmatrix*} = \begin{bmatrix*}[c] v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix*} + \begin{bmatrix*}[c] u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix*} = \bs{v} + \bs{u} $$

■


Exercise 1

Calculate $\bs{u} + \bs{v}$ and $\bs{u} - 2\bs{v}$: $$ \bs{u} = \begin{bmatrix*}[r] -1 \\ 2 \end{bmatrix*}, \qquad \bs{v} = \begin{bmatrix*}[r] -3 \\ -1 \end{bmatrix*} $$

Answer
$$ \bs{u} + \bs{v} = \begin{bmatrix*}[r] -1 \\ 2 \end{bmatrix*} + \begin{bmatrix*}[r] -3 \\ -1 \end{bmatrix*} = \begin{bmatrix*}[r] -1 - 3 \\ 2 -1 \end{bmatrix*} = \begin{bmatrix*}[r] -4 \\ 1 \end{bmatrix*} $$ $$ \bs{u} - 2\bs{v} = \begin{bmatrix*}[r] -1 \\ 2 \end{bmatrix*} - 2 \begin{bmatrix*}[r] -3 \\ -1 \end{bmatrix*} = \begin{bmatrix*}[r] -1 \\ 2 \end{bmatrix*} + \begin{bmatrix*}[r] 6 \\ 2 \end{bmatrix*} = \begin{bmatrix*}[r] -1 + 6 \\ 2 + 2 \end{bmatrix*} = \begin{bmatrix*}[r] 5 \\ 4 \end{bmatrix*} $$

■


Exercise 11

Is b a linear combination of a1, a2 and a3? $$ \bs{a}_1 = \begin{bmatrix*}[r] 1 \\ -2 \\ 0 \end{bmatrix*}, \quad \bs{a}_2 = \begin{bmatrix*}[r] 0 \\ 1 \\ 2 \end{bmatrix*}, \quad \bs{a}_3 = \begin{bmatrix*}[r] 5 \\ -6 \\ 8 \end{bmatrix*}, \quad \bs{b} = \begin{bmatrix*}[r] 2 \\ -1 \\ 6 \end{bmatrix*}, $$

Answer
We can write this as an augmented matrix and see if it has a solution. $$ \begin{align} \big[\bs{a}_1\;\; \bs{a}_2\;\; \bs{a}_3\;\; \bs{b}\big] \;&=\; \begin{bmatrix*}[rrrr] 1 & 0 & 5 & 2 \\ -2 & 1 & -6 & -1 \\ 0 & 2 & 8 & 6 \end{bmatrix*} \\ &\; \\ II + 2I &\sim\; \begin{bmatrix*}[rrrr] 1 & 0 & 5 & 2 \\ 0 & 1 & 4 & 3 \\ 0 & 2 & 8 & 6 \end{bmatrix*} \\ &\; \\ III - 2II &\sim\; \begin{bmatrix*}[rrrr] 1 & 0 & 5 & 2 \\ 0 & 1 & 4 & 3 \\ 0 & 0 & 0 & 0 \end{bmatrix*} \end{align} $$ We have the following solution set: $$ \left\{ \begin{array}{l} x_1 = 2 - 5x_3 \\ x_2 = 3 - 4x_3 \\ x_3 \;\text{is free} \end{array} \right. $$ In other words, there are an infinite number of solutions. Let's fix $x_1 = 0$, then $x_1 = 2$ and $x_2 = 3$. Verifying: $$ 2\bs{a}_1 + 3\bs{a}_2 = 2 \begin{bmatrix*}[r] 1 \\ -2 \\ 0 \end{bmatrix*}, + 3 \begin{bmatrix*}[r] 0 \\ 1 \\ 2 \end{bmatrix*} = \begin{bmatrix*}[r] 2 \\ -4 \\ 0 \end{bmatrix*} + \begin{bmatrix*}[r] 0 \\ 3 \\ 6 \end{bmatrix*} = \begin{bmatrix*}[r] 2 \\ -1 \\ 6 \end{bmatrix*} = \bs{b} $$

If $x_3 = 1$, then $x_1 = 2 - 5 = -3$ and $x_2 = 3 - 4 = -1$, so: $$ (-3)\bs{a}_1 + (-1)\bs{a}_2 + \bs{a}_2 = (-3) \begin{bmatrix*}[r] 1 \\ -2 \\ 0 \end{bmatrix*} + (-1) \begin{bmatrix*}[r] 0 \\ 1 \\ 2 \end{bmatrix*} + \begin{bmatrix*}[r] 5 \\ -6 \\ 8 \end{bmatrix*} = \begin{bmatrix*}[r] -3 \\ 6 \\ 0 \end{bmatrix*} + \begin{bmatrix*}[r] 0 \\ -1 \\ -2 \end{bmatrix*} + \begin{bmatrix*}[r] 5 \\ -6 \\ 8 \end{bmatrix*} = \begin{bmatrix*}[r] 2 \\ -1 \\ 6 \end{bmatrix*} = \bs{b} $$

■


Exercise 13

Determine if b is a linear combination of the columns in matrix A. $$ A = \begin{bmatrix*}[rrr] 1 & -4 & 2 \\ 0 & 3 & 5 \\ -2 & 8 & -4 \end{bmatrix*}, \quad \bs{b} = \begin{bmatrix*}[r] 3 \\ -7 \\ -3 \end{bmatrix*} $$

Answer
We start with the augmented matrix. $$ \begin{bmatrix*}[rrrr] 1 & -4 & 2 & 3 \\ 0 & 3 & 5 & -7 \\ -2 & 8 & -4 & -3 \end{bmatrix*} $$ III + 2I $$ \begin{bmatrix*}[rrrr] 1 & -4 & 2 & 3 \\ 0 & 3 & 5 & -7 \\ 0 & 0 & 0 & 3 \end{bmatrix*} $$ Here we can see that we have an inconsistent system, so there are no solutions. So, we can conclude that b is not a linear combinations of the matrix columns.

■


Exercise 15

List five vectors in Span$\{\bs{v}_1, \bs{v}_2\}$ and list the associated weights. $$ \bs{v}_1 = \begin{bmatrix*}[r] 7 \\ 1 \\ -6 \end{bmatrix*}, \quad \bs{v}_2 = \begin{bmatrix*}[r] -5 \\ 3 \\ 0 \end{bmatrix*} $$

Answer
We are working in $\R^3$, so the span of two vectors will be a 2D plane. I'll list two. Set weights c1 = 1, c2 = 1. $$ \bs{v}_1 + \bs{v}_2 = \begin{bmatrix*}[r] 7 \\ 1 \\ -6 \end{bmatrix*} + \begin{bmatrix*}[r] -5 \\ 3 \\ 0 \end{bmatrix*} = \begin{bmatrix*}[r] 2 \\ 4 \\ -6 \end{bmatrix*} $$ Set weights c1 = 2, c2 = -1. $$ 2\bs{v}_1 - \bs{v}_2 = 2\begin{bmatrix*}[r] 7 \\ 1 \\ -6 \end{bmatrix*} - \begin{bmatrix*}[r] -5 \\ 3 \\ 0 \end{bmatrix*} = \begin{bmatrix*}[r] 14 \\ 2 \\ -12 \end{bmatrix*} - \begin{bmatrix*}[r] -5 \\ 3 \\ 0 \end{bmatrix*} = \begin{bmatrix*}[r] 24 \\ -1 \\ -12 \end{bmatrix*} $$

■


Exercise 19

Give a geometric description of Span$\{\bs{v}_1, \bs{v}_2\}$ for the vectors $$ \bs{v}_1 = \begin{bmatrix*}[r] 8 \\ 2 \\ -6 \end{bmatrix*},\quad \bs{v}_2 = \begin{bmatrix*}[r] 12 \\ 3 \\ -9 \end{bmatrix*} $$

Answer
To start off, we can simplify them. Since we are scaling both vectors belong to the same span, and in turn spans the same plane. So we divide them by 2 and 3 respectively and remame to u. $$ \bs{u}_1 = \begin{bmatrix*}[r] 4 \\ 1 \\ -3 \end{bmatrix*},\quad \bs{u}_2 = \begin{bmatrix*}[r] 4\\ 1 \\ -3 \end{bmatrix*} $$ Now we see that they lie on the same line, and so this does not span a plane in $\R^3$, but instead it spans a line going through the origin and the point (4, 1, -3).

■