Chapter 2 - Metric Spaces

2.6 Convergence. Open and Closed Sets

Main:	Index
Previous:	2.5 Basic Concepts
Next:	2.7 Complete Metric Spaces

Results

Open Ball
An open sphere/ball $S(x_0, r)$ is the set of points $x\in X$ satisfying the inequality: $$ \rho(x_0, x) < r. $$ where $\rho$ is a metric. The fixed point $x_0$ is the center of the sphere, and $r$ is the radius.



Closed Ball
An closed sphere/ball $S[x_0, r]$ is the set of points $x\in X$ satisfying the inequality: $$ \rho(x_0, x) \leq r. $$ where $\rho$ is a metric. The fixed point $x_0$ is the center of the sphere, and $r$ is the radius.



Contact Point and Closure
A point $x\in X$ is a contact point for a set $M\subset X$ if every neighborhood of $x$ (epsilon-ball around $x$) contains at least one point of $M$. (For instance, the point 1 is a contact point for $(0,1)$).

The set of all contact points is called the closure of $M$ and denoted by $[M]$. For instance, $[(0,1)] = [0,1]$.




The closure operator $[\cdot]$ has the following properties:

1) If $M\subset N$ then $[M]\subset[N]$
2) $[[M]] = [M]$
3) $[M\cup N] = [M]\cup[N]$
4) $[\emptyset] = \emptyset$



Convergence
A sequence $\{x_n\}$ in a metric space converges to a point $x\in X$ if every neighborhood $O_\eps(x)$ contains all points of the sequence after some $N\in\N$. The point $x$ is called the limit of the sequence $\{x_n\}$.




A necessary and sufficient condition for a point $x$ to be a contact point of a set $M$ is that there exist a sequence $\{x_n\}$ of points of $M$ converging to $x$.




A necessary and sufficient condition for a point $x$ to be a limit point of a set $M$ is that there exist a sequence $\{x_n\}$ of distinct points of $M$ converging to $x$.



Dense subset
Let $A$ and $B$ be two subsets of $X$. $A$ is dense in $B$ if $[A]\supset B$. And $A$ is said to be dense everywhere if $[A] = X$.
(Example: $\Q$ is dense everywhere in $\R$.)




A metric space is said to be separable if it has a countable everywhere dense subset.



Closed Sets
A subset $M$ of a metric space $(X,\rho)$ is closed if it coincides with its own closure, that is, $[M] = M$. Or in other words, it is closed if it contains all it's limit points.




The intersection of an arbitrary number of closed sets is closed. The union of a finite number of closed sets is closed.



Open Sets
A point $x$ is called an interior point of a set $M$ if $x$ has a neighborhood $O_\eps(x)\subset M$, i.e. it has a neighborhood consisting entirely of points of $M$. A set is said to be open if all its points are interior points.




A subset $M$ of a metric space $(X, \rho)$ is open if and only if its complement $X-M$ is closed.




The empty set $\emptyset$ and the whole space $X$ are open sets. (Note: they also satisfy the conditions for being closed sets, so they are both).




The union of an arbitrary number of open sets is open. The intersection of a finite number of open sets is open.




Every open set $G$ on the real line is the union of a finite or countable system of pairwise disjoint open intervals.




Every closed set on the real line can be obtained by deleting a finite or coutnable system of pairwise disjoint intervals from the line.



Continuity
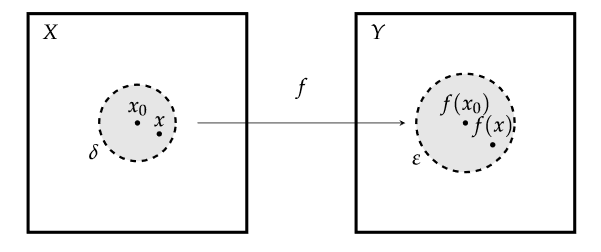
Let $f$ be a mapping from $X$ to $Y$ (metric spaces). The function $f$ is continuous if for all $\eps > 0$ there exists some $\delta > 0$ such that $$ \rho(x_0, x) < \delta \;\Longrightarrow\; \rho'(f(x_0), f(x)) < \eps. $$ Informally: Whenever we select an $x$ from within the $\delta$-ball in $X$, the mapping will lie inside the $\eps$-ball in $Y$. Here is an illustration.

Problem 1

Give an example of a metric space $(X, \rho)$ and two open spheres $S(x, r_1)$ and $S(y, r_2)$ in $X$ such that $S(x,r_1)\subset S(y, r_2)$ although $r_1 > r_2$.

Solution.
Let $X = U(1)\subset\R^2$ where $U(1)$ denotes the unit circle, i.e. the set $\{(x,y)\in\R\,|\, x^2 + y^2 < 1\}$. The distance is the standard Euclidean metric: $$ \rho(x,y) = \sqrt{x^2 + y^2} $$ Now, select two points $x = y = (0,0)$, and set $r_1 = 2$ and $r_2 = 1$. Then $r_1 > r_2$, but $S(x,r_1)\subset S(y, r_2)$. (The sets are restricted to a subspace, and in that subspace they are the same).

Problem 2

Prove that every contact point of a set $M$ is either a limit point of $M$ or an isolated point of $M$.

Proof.
By Theorem 2, for some contact point $y$ for $M$, there exists a sequence $\{x_n\}$ of points in $M$ that converges to $y$. By the definition of convergence, for every epsilon-ball $O_\eps(y)$ there is some $N\in\N$ such that all points in $\{x_n\}$ after $x_N$ lie inside $O_\eps(y)$. There are two exhaustive possibilities,
1) Every $O_\eps(y)$ contains a single point, in which case $y$ is an isolated point.
2) Every $O_\eps(y)$ contains an infinite amount of points, in which case $y$ is a limit point.

Problem 3

Prove that if $x_n\rightarrow x$ and $y_n\rightarrow y$ as $n\rightarrow \infty$, then $\rho(x_n, y_n)\rightarrow\rho(x, y)$.

Proof.
Using the identity from Problem 1 in section 2.5: $$ |\rho(x, z) - \rho(y, u)| \leq \rho(x, y) + \rho(z, u). $$ In our case, we set $x = x_n$, $z = y_n$, $y = x$ and $u = y$: $$ |\rho(x_n, y_n) - \rho(x, y)| \leq \rho(x_n, x) + \rho(y_n, y). $$ Taking the limit: $$ \lim_{n\rightarrow\infty}|\rho(x_n, y_n) - \rho(x, y)| \leq \lim_{n\rightarrow\infty} \Big(\rho(x_n, x) + \rho(y_n, y)\Big) = 0 $$ Which leaves us with: $$ \lim_{n\rightarrow\infty}|\rho(x_n, y_n) - \rho(x, y)| \leq 0 $$ which means $\rho(x_n, y_n)\rightarrow\rho(x, y)$ as $n\rightarrow\infty$.

Problem 4

Let $f$ be a mapping from one metric $(X,\rho)$ space to another $(Y,\rho')$, $f: X\rightarrow Y$. Prove that $f$ is continuous at a point $x_0$ if and only if the sequence $\{y_n\} = \{f(x_n)\}$ converges to $y = f(x_0)$ when $x_n\rightarrow x_0$.

Proof.
Showing implication both ways.

$\Rightarrow$) Assume $f$ is continuous and $x_n\rightarrow x_0$. For any $\eps > 0$, then $\rho'(f(x_n), f(x_0)) < \eps$ since, by continuity of $f$, there exists some $\delta > 0$ such that $\rho(x_n, x_0) < \delta$, which follows by convergence of $\{x_n\}$ (set $\delta = \eps_2 > 0)$. This shows that $f(x_n)\rightarrow f(x_0)$.

$\Leftarrow$) Assume that $x_n\rightarrow x_0$ and that $f(x_n)\rightarrow f(x_0)$ as $n\rightarrow\infty$. For any $\eps > 0$ we can find some $N_1\in\N$ such that $\rho'(f(x_n), f(x_0)) < \eps$ whenever $n\geq N_1$ and some $N_2\in\N$ such that $\rho(x_n, x_0) < \eps$ whenever $n\geq N_2$. Let $\delta = \eps$, then $\rho(x_n, x_0) < \delta$ implies that $\rho'(f(x_n), f(x_0)) < \eps$ for $n\geq \max(N_1, N_2)$ and we can conclude that $f$ is continuous.

NOTE: In the last part, we showed continuity only for points in the sequence $\{x_n\}$ and not any $x$ close to $x_0$. Do we need an argument on limit points and isolated points?

Problem 5

Prove the statements.

a) The closure of any set $M$ is closed.

Proof.
Any closed set coincides with its closure, and since by Theorem 1, $[[M]] = [M]$, then $[M]$ is a closed set.

b) $[M]$ is the smallest closed set containing $M$.

Proof.
Assume $M$ is a closed set. Then $[M] = M$ which obviously is the smallest set containing $M$.

Now assume that $M$ is an open set. Let $C$ be some arbitrary closed set such that $M\subset C$. Assume $y\in[M]$, then it is a limit point for $M$. Since $M\subset C$ and a closed set contains all its limit points, it follows that $y\in C$, which shows that $[M]\subset C$. Since any closed set $C$ containing $M$ also contains $[M]$, it shows that $[M]$ is the smallest closed set.

Problem 6

Is the union of infinitely many closed sets necessarily closed? How about the intersection of infinitely many open sets? Give examples.

Proof.
The countable union of closed sets can be an open set, as shown in Problem 7, in section 1.1. $$ \bigcup_{n=1}^\infty \left[a + \frac{1}{n}, b - \frac{1}{n}\right] = (a, b) $$ And the countable intersection of open sets can be a closed sets, also shown in Problem 7. $$ \bigcup_{n=1}^\infty \left(a - \frac{1}{n}, b + \frac{1}{n}\right) = [a, b] $$

Problem 7

Prove directly that the point 1/4 belongs to the Cantor set, $F$, although it is not an end point of any of the open intervals deleted in constructing $F$.

Proof.
As noted in the text, any $x\in[0,1]$ can be written in ternary notation: $$ x = \frac{a_1}{3} + \frac{a_2}{3^2} + \ldots + \frac{a_2}{3^n} + \ldots, $$ where $a_i$ can only take values $0, 1, 2$. The $x$ belongs to $F$ if and only if none of the $a_i$ equals 1. If write 1/4 in this form it becomes: $$ \frac{1}{4} = \frac{0}{3} + \frac{2}{3^2} + \frac{0}{3^3} + \frac{2}{3^4} + \frac{0}{3^5} + \frac{2}{3^6} + \ldots, $$ or in decimal form: $$ \frac{1}{4} = 0.0202020202\ldots $$ Since there are no 1s, this shows that $1/4\in F$.

Problem 8

Let $F$ be the Cantor set. Prove the following.

(a) The points of the first kind; $$ 0, 1, \frac{1}{3}, \frac{2}{3}, \frac{1}{9}, \frac{2}{9}, \frac{7}{9}, \frac{8}{9},\ldots $$ form an everywhere dense subset of $F$.

Proof.
Define the set of points to be $G$. We want to show that $F\subset [G]$, and we do that by showing that any point in $F$ is a limit point of $G$.

Assume $x\in F$. For any $\eps > 0$ we will consider the $\eps$-ball, which in this case is the interval: $(x - \eps, x + \eps)$. In this interval, we can find some endopints from $G$ satisfying: $$ x - \eps < \frac{3k}{3^n} < \frac{3k+1}{3^n} < x + \eps $$ for some $k,n\in\N$ (a similar argument can be used for any expression of the general formula of the Cantor endpoints). But once we have identified some endpoints that are in the set, we can find an infinite amount of endpoints that are between them, from the Cantor set construction. This means $(x-\eps, x+\eps)$ contains an infinite amount of points from $G$, which means that $x\in F$ is a limit point for $G$.

The closure of a set will contain all its limit points, so since $x\in F$ is a limit point for $G$, then $x\in[G]$. Since $x$ was an arbitrary point, this shows that $F\subset [G]$, which also shows that $G$ is an everywhere dense subset of $F$.

(b) The numbers of the form $t_1 + t_2$, where $t_1,t_2\in F$, fill the whole interval $[0,2]$.

Skipped for now...

Problem 9

Given a metric space $(X,\rho)$, let $A\subset X$ and $x\in X$. Then the number $$ \rho(A, x) = \inf_{a\in A}\rho(a, x) $$ is called the distance between $A$ and $x$. Prove the following statements:

(a) $x\in A$ implies $\rho(A, x) = 0$, but not conversely.

Proof.
Assume $x\in A$. Since the distance is nonnegative, $\inf_{a\in A}\rho(a, x)\geq 0$ then $a = x$ so $\inf_{a\in A}\rho(a, x) = \rho(x, x) = 0$.

To show that the converse is not true consider the following counterexample. Let $X = \R$, let $A = (0,1)$ and let $x = 1$. Then $x\not\in A$, but for any $\eps > 0$ we can find some $a\in A$ such that $|a - 1| < \eps$, which means $\inf_{a\in A}\rho(a, x) = 0$.

(b) $\rho(A, x)$ is a continuous function of $x$ (for fixed $A$).

Proof.
Defining $f(x) := \rho(x, A)$.

If $V\subset X$ is an open set containing $f(x)$, then $f$ is continuous if there is some open set $U\subset X$ such that $x\in U$ and $f(U)\subset V$.

Assume $f(x)\in V$ for some open set $V$. Then for any $\eps > 0$ there exists an epsilon-ball such that $O_\eps(f(x))\subset V$. Now, our claim is that there exists some open set $U = O_{\frac{\eps}{2}}(x)$ such that $f(U) \subset O_\eps(f(x))\subset V$. Let $y\in A$ and $z\in O_{\frac{\eps}{2}}(x)$, which means that the distance from $z$ to $x$ is smaller than $\eps/2$. By the triangle inequality: $$ \rho(y, z) \leq \rho(x, y) + \rho(x, z) $$ $$ \rho(x, y) \leq \rho(x, z) + \rho(z, y). $$ By the property of the infimum; $$ \rho(z, A) \leq \rho(x, A) + \rho(x, z) < \rho(x, A) + \frac{\eps}{2} $$ $$ \rho(x, A) \leq \rho(x, z) + \rho(z, A) < \rho(z, A) + \frac{\eps}{2} $$ Or directly, $$ \rho(z, A) < \rho(x, A) + \frac{\eps}{2} $$ $$ \rho(x, A) < \rho(z, A) + \frac{\eps}{2} $$ Which, when combined, shows us that: $$ \rho(x, A) - \frac{\eps}{2} < \rho(z, A) < \rho(x, A) + \frac{\eps}{2} $$ which shows that $f(z)\in O_\eps)f(x) \subset V$, and that $f(U)\subset V$ which proves that $f$ is continuous.

(c) $\rho(A, x) = 0$ if and only if $x$ is a contact point of $A$.

Proof.
$\Rightarrow$) Assume $\rho(A, x) = 0$. Then for any $\eps > 0$, the point $O_\eps(x)$ will contain points in $A$ and is therefore a contact point of $A$.

$\Leftarrow$) Assume $x\in A$ is a contact point. Assume further that $A$ is closed. Then $x\in A$, since a closed point contains all its contact points. Then by (a), the distance from $A$ to $x$ is 0. Assume now that $A$ is open. Let $x$ be a contact point. By definition, for any $\eps > 0$ the ball $O_\eps(x)$ will contain points from $A$, so $\rho(A, x) < \eps$. Since this is true for any $\eps > 0$, this means that $\rho(A, x) = 0$.

(d) $[A] = A\cup M$, where $M$ is the set of all points $x$ such that $\rho(A, x) = 0$.

Proof.
$\subset$) Assume $x\in[A]$. Since $[A]$ is closed it contains all its contact points, so $\rho(A, x) = 0$, which means $x\in M \subset A\cup M$. Hence $[A]\subset A\cup M$.

$\supset$) Assume $x\in A$. Since $A\subset[A]$ then $x\in [A]$. Assume now that $x\in M$ and $x\not\in A$. Then by definition of $M$, $\rho(A, x) = 0$ which means $x$ is a contact point for $A$ by (c), which also means $x\in[A]$. It follows that $A\cup M\subset[A]$.

Problem 10

Let $A$ and $B$ be two subsets of a metric space $(X,\rho)$. Then the number $$ \rho(A, B) = \inf_{a\in A, b\in B}\rho(a, b) $$ is called the distance between $A$ and $B$. Show that $\rho(A, B) = 0$ if $A\cap B\not=\emptyset$, but not conversely.

Proof.
Let $x\in A\cap B$. Then by 9(a), $\rho(x, A) = 0$ and $\rho(x, B) = \rho(B, x) = 0$. From the triangle inequality, $\rho(A, B) \leq \rho(A, x) + \rho(x, B) = 0 + 0 = 0$ which shows that $\rho(A, B) = 0$.

Showing that the converse is not true with a counterexample. Let $X = \R$, let $A = (0,1)$ and let $B = [1, 2)$. Then as shown above, $\rho(A, 1) = 0$ and since $1\in B$, $\rho(A, B) = 0$.

Problem 11

Skipped...

Problem 12

Skipped...