Chapter 1 - Set Theory
1.1 Sets and Functions
| Main: | Index |
| Previous: | Index |
| Next: | 1.2 Equivalent Sets. Power of a Set |
Problem 1
If $A\cup B = A$ and $A\cap B = A$, then $A = B$.Proof.
In order to prove that two sets are equal, we show that $A\subset B$ and $A\supset B$.
$\subset$). Since $A = A\cap B$ and $A\cap B\subset B$ , then $A \subset B$.
$\supset$). Since $B \subset A\cup B$ and $A\cup B = A$, then $B\subset A$.
By inclusion both ways, $A = B$.
■
Problem 2
Show that in general $(A-B)\cup B \not= A$.This can be shown by finding a counterexample. A simple case is when the sets are disjoint. If we set $A = \{a\}$ and $B = \{b\}$ where $a\not= b$, then $$ A - B = \{a\} - \{b\} = \{a\} = A. $$ And then: $$ (A-B)\cup B = A\cup B = \{a\}\cup\{b\} = \{a,b\} \not= \{a\} = A. $$
Problem 3
Let $A = \{2, 4, \ldots, 2n, \ldots\}$ and $B = \{3, 6, \ldots, 3n, \ldots\}$. Find $A\cap B$ and $A-B$.$A$ is the set of all numbers divisible by 2 (even numbers), and $B$ is the set of all numbers divisible by 3.
The set $A\cap B$ contains the numbers that are divisible by both 2 and 3. The first elements will be $\{6, 12, 18, \ldots\}$ so it is clear that it will contain all numbers divisible by 6. $$ A\cap B = \{6, 12, 18, \ldots, 6n, \ldots\}. $$
The set $A-B$ will contain all even numbers, except those that are divisible by 3. The terms become $\{2, 4, 8, 10, \ldots\}$. We can express this generally by defining: $$ g(n) = \left\{ \begin{matrix} 1, & \text{$n$ is odd} \\ 2, & \text{$n$ is even} \end{matrix} \right. $$ And so we get: $$ A - B = \{2, 4, 8, 10, \ldots, 3n - g(n),\ldots \} $$
Problem 4
Prove that:(a) $(A-B)\cap C = (A\cap C)-(B\cap C)$
Proof.
Assuming that $x\in (A-B)\cap C$ for some arbitrary $x$. We get the following equivalent statements. $$ \begin{aligned} x\in (A-B)\cap C &\Leftrightarrow x\in A\cap B^c\cap C \\ &\Leftrightarrow x\in A\cap B^c\cap C \cap C \\ &\Leftrightarrow x\in A\cap C\cap B^c \cap C \\ &\Leftrightarrow x\in A\cap C\;\text{and}\; x\in B^c \cap C \\ &\Leftrightarrow x\in A\cap C\;\text{and}\; x\in B^c \;\text{and}\; x\in C \\ &\Leftrightarrow x\in A\cap C\;\text{and}\; x\not\in B \;\text{and}\; x\in C \\ &\Leftrightarrow x\in A\cap C\;\text{and}\; x\not\in B\cap C\\ &\Leftrightarrow x\in (A\cap C) - (B\cap C) \end{aligned} $$ which shows that the statements are equivalent. (Used indempotence and the commutative property in steps 2 and 3, as well as the definition of set difference).
■
(b) $A\bigtriangleup B = (A\cup B)-(A\cap B)$
Proof.
Recall that the symmetric difference is defined in the following way. $$ A\bigtriangleup B = (A - B)\cup(B - A). $$ We will prove this by assuming some arbitrary point $x$ is included in the right hand side and show that this is equivalent to it being in the left hand side. To make a step including the distributive property easier to read, we will define $W = (A\cup B)$. $$ \begin{align} x\in (A\cup B)-(A\cap B) &\Leftrightarrow x\in (A\cup B)\cap(A\cap B)^c \\ &\Leftrightarrow x\in (A\cup B)\cap(A^c\cup B^c) \\ &\Leftrightarrow x\in W\cap(A^c\cup B^c) \\ &\Leftrightarrow x\in (W\cap A^c)\cup (W\cap B^c) \\ &\Leftrightarrow x\in ((A\cup B)\cap A^c)\cup ((A\cup B)\cap B^c) \\ &\Leftrightarrow x\in (A\cap A^c)\cup(B\cap A^c)\cup (A\cap B^c)\cup (B\cap B^c) \\ &\Leftrightarrow x\in \emptyset\cup(B\cap A^c)\cup (A\cap B^c)\cup \emptyset \\ &\Leftrightarrow x\in (B\cap A^c)\cup (A\cap B^c) \\ &\Leftrightarrow x\in (A\cap B^c)\cup (B\cap A^c) \\ &\Leftrightarrow x\in (A - B)\cup (B - A) \\ &\Leftrightarrow x\in A\bigtriangleup B \end{align} $$
■
Problem 5
Prove that: $$ \bigcup_\alpha A_\alpha - \bigcup_\alpha B_\alpha \subset \bigcup_\alpha (A_\alpha - B_\alpha). $$Proof.
We just need to prove implications one way. For some arbitrary point $x$. $$ \begin{align} x\in \bigcup_\alpha A_\alpha - \bigcup_\alpha B_\alpha &\Rightarrow x\in \bigcup_\alpha A_\alpha\cap\Big[\bigcup_\alpha B_\alpha\Big]^c \\ &\Rightarrow x\in \bigcup_\alpha A_\alpha\cap\Big[\bigcap_\alpha B^c_\alpha\Big] \\ &\Rightarrow x\in \bigcup_\alpha A_\alpha \;\text{and}\; x\in\bigcap_\alpha B^c_\alpha \end{align} $$ By assumption, there is at least one $\alpha$ such that $x\in A_\alpha$. Let us fix that index and call it $\beta$. Since $x\in B_\alpha^c$ for all $\alpha$, we also have $x\in B^c_\beta$. $$ \begin{align} x\in A_\beta \;\text{and}\; x\in B_\beta^c &\Rightarrow x\in A_\beta\cap B_\beta^c \\ &\Rightarrow x\in A_\beta - B_\beta \\ &\Rightarrow x\in \bigcup_\alpha (A_\alpha - B_\alpha) \end{align} $$ Since $x$ was some arbitrary point, the inclusion has been proved.
We will also give a counterexample to show that the reverse inclusion doesn't need to be true. Define the index set to be $\alpha = \{1, 2\}$. Also, define the sets: $$ A_1 = \{1, 2\},\quad B_1 = \{1\} $$ $$ A_2 = \{1, 2\},\quad B_2 = \{2\} $$ Using these, we get: $$ \begin{align} \bigcup_\alpha (A_\alpha - B_\alpha) &= (A_1 - B_1) \cup (A_2 - B_2) \\ &= \Big(\{1,2\} - \{1\}\Big) \cup \Big(\{1,2\} - \{2\}\Big) \\ &= \{2\}\cup\{1\} \\ &= \{1, 2\}. \end{align} $$ But now, on the left hand side: $$ \begin{align} \bigcup_\alpha A_\alpha - \bigcup_\alpha B_\alpha &= (A_1 \cup A_2) - (B_1 \cup B_2) \\ &= \{1,2\}\cup\{1,2\} - \{1\}\cup\{2\} \\ &= \{1,2\} - \{1,2\} \\ &= \emptyset. \end{align} $$ This shows that the reverse inclusion is not necessarily true.
■
Problem 6
Let $A_n$ be the set of all positive integers divisible by $n$. Find the sets $$ \text{(a)}\;\bigcup_{n=2}^\infty A_n $$Proof.
The first element of each $A_n$ will be $n\in\mathbb{N}$. For $2,3$ and any arbitrary $m\in \mathbb{N}$: $$ A_2 = \{2,\ldots\},\quad A_3 = \{3,\ldots\},\quad A_m = \{m,\ldots\} $$ If $m$ is even, the set $A_m$ is already contained in $A_2$, but we are not concerned with any repetition. For the first two sets: $$ A_{2,3} = A_2\cup A_3 = \{2, 3, \ldots\}, $$ where $$ A_{2,m} = \bigcup_{n=2}^m A_n. $$ After we have joined the first $k$ sets and join $A_{k+1}$: $$ A_{2,k+1} = A_{2,k}\cup A_{k+1} = \{2,3,\ldots,k,\ldots\}\cup\{k+1,\ldots\} = \{2,3,\ldots,k,k+1,\ldots\} $$ where we only add new values when $k+1$ is prime. From this argument it should be clear that we keep adding in new points until we have filled up the union with the natural numbers, except for $1$. We define: $$ \mathbb{N}_2 = \mathbb{N} - \{1\} = \{2,3,4,\ldots\}. $$ Our claim is that: $$ \bigcup_{n=2}^\infty A_n = \mathbb{N}_2, $$ which we prove by showing that they are subsets of each other. Suppose $m\geq 2$ is some arbitrary natural number.
$$ \subset)\; m\in \bigcup_{n=2}^\infty A_n \Longrightarrow m\in A_m \Longrightarrow m\in \mathbb{N}_2 \Longrightarrow \bigcup_{n=2}^\infty A_n\subset \mathbb{N}_2, $$ since $m\geq 2$. $$ \supset)\; m\in \mathbb{N}_2 \Longrightarrow m\in A_m \Longrightarrow m\in \bigcup_{n=2}^\infty A_n \Longrightarrow \mathbb{N}_2\subset\bigcup_{n=2}^\infty A_n $$ By inclusion both ways, we have shown that $$ \bigcup_{n=2}^\infty A_n = \mathbb{N}_2. $$
■
$$ \text{(b)}\;\bigcap_{n=2}^\infty A_n $$
Proof.
We focus on the first element of the sets again. For $2,3$ and any arbitrary $m\in \mathbb{N}$: $$ A_2 = \{2,\ldots\},\quad A_3 = \{3,\ldots\},\quad A_m = \{m,\ldots\} $$ Using a similar definition as earlier: $$ A_{2,m} = \bigcap_{n=2}^m A_n. $$ When intersecting $A_2$ and $A_3$, we get: $$ A_{2,3} = A_2\cap A_3 = \{2,\ldots\}\cap\{3,\ldots\} = \{3,\ldots\}. $$ After intersecting the first $k$ sets and intersecting that with $A_{k+1}$: $$ A_{2,k+1} = A_{2,k}\cap A_{k+1} = \{k,\ldots\}\cap\{k+1,\ldots\} = \{k+1,\ldots\}. $$ In this case the sets become smaller and smaller, and we will end up with the empty set. Our claim: $$ \bigcap_{n=2}^\infty A_n = \emptyset $$ We prove this by showing that the intersection is empty. Using proof by contradiction, for some $k\in\mathbb{N}$: $$ k\in \bigcap_{n=2}^\infty A_n $$ However, $k$ is not included in the intersection, since $k\not\in A_{k+1}$. Our assumption cannot be true, and so we must conclude that $$ \bigcap_{n=2}^\infty A_n = \emptyset. $$
■
Problem 7
Find the following sets. $$ \text{a)}\; \bigcup_{n=1}^\infty\Big[a + \frac{1}{n}, b - \frac{1}{n}\Big]. $$Proof.
To simplify the notation, we will define each interval as: $$ I_n = \Big[a + \frac{1}{n}, b - \frac{1}{n}\Big]. $$ The first three intervals are: $$ I_1 = \Big[a + 1, b - 1\Big],\quad I_2 = \Big[a + \frac{1}{2}, b - \frac{1}{2}\Big],\quad I_3 = \Big[a + \frac{1}{3}, b - \frac{1}{3}\Big] $$ As $n$ gets bigger, so do the intervals. Here is a sketch to illustrate:
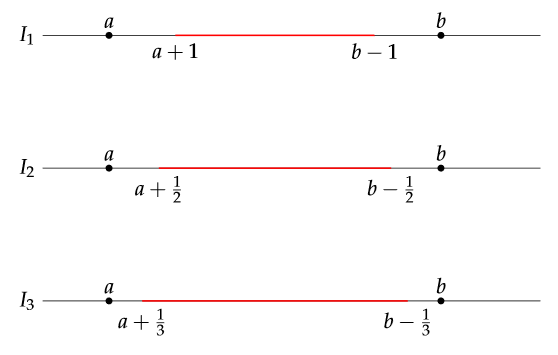
By taking the union of the two first sets: $$ I_1\cup I_2 = I_2 $$ since $I_1\subset I_2$. Since the interval is increasing in size, we also get $$ \bigcup_{n=1}^{k+1} I_n = I_{k+1}. $$ Taking the countable union results in the following: $$ \bigcup_{n=1}^\infty\Big[a + \frac{1}{n}, b - \frac{1}{n}\Big] = %\lim_{n\rightarrow\infty} \Big[a + \frac{1}{n}, b - \frac{1}{n}\Big] = (a, b). $$ This is from a general property in metric spaces which states that every open set is a countable union of closed sets.
For any $\varepsilon > 0$, $a+\varepsilon\in \bigcup_{n=1}^\infty I_n$ since we can find some $N\in\mathbb{N}$ such that $a+1/N < a + \varepsilon$, so $a\not\in I_n$ for all $n$.
■
$$ \text{b)}\; \bigcap_{n=1}^\infty\Big(a - \frac{1}{n}, b + \frac{1}{n}\Big). $$
Proof.
We will denote each interval as $I_n$. The first three intervals are: $$ I_1 = \Big(a - 1, b + 1\Big),\quad I_2 = \Big(a - \frac{1}{2}, b + \frac{1}{2}\Big),\quad I_3 = \Big(a - \frac{1}{3}, b + \frac{1}{3}\Big) $$ Here is a sketch to illustrate:
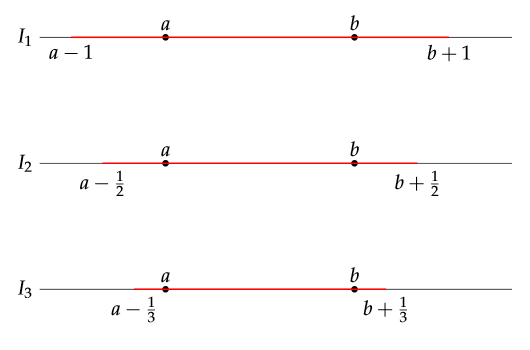
As the sets, or intervals, are decreasing and since $I_1 \subset I_2$, we get: $$ I_1\cap I_2 = I_2, $$ and in general, $$ I_1\cap I_2\cap\ldots\cap I_k\cap I_{k+1} = I_{k+1}. $$ Taking an infinite amount of intersections gives: $$ \bigcap_{n=1}^\infty\Big(a - \frac{1}{n}, b + \frac{1}{n}\Big) = [a, b]. $$ This is from a general property in metric spaces which states that every closed set is a countable intersection of open sets.
For any $\varepsilon > 0$, $a-\varepsilon\not\in \bigcap_{n=1}^\infty I_n$ since we can find some $N\in\mathbb{N}$ such that $a-\varepsilon\not\in I_N$, but $a\in I_n$ for all $n$.
■
Problem 8
Let $A_\alpha$ be the set of points on the curve $$ y = \frac{1}{x^\alpha},\;\;0< x <\infty. $$ We will determine the intersection: $$ \bigcap_{\alpha\geq 1} A_\alpha. $$ Sketching the graphs for $\alpha = 1,\ldots, 6$, which gives us a hint to the solution.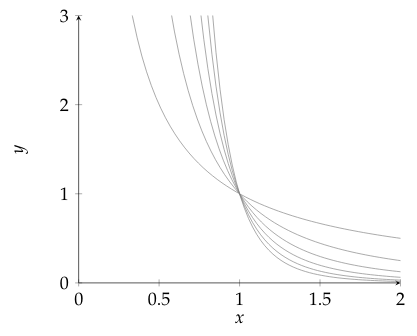
Expressing the set explicitly; $A_\alpha = \{(x, 1/x^\alpha)\;|\; x > 0\}$, so each element contains a point corresponding to the cartesian coordinates. The first two sets are: $$ A_1 = \{(x, 1/x)\;|\; x > 0\} $$ $$ A_2 = \{(x, 1/x^2)\;|\; x > 0\} $$ When considering the intersection $A_1\cap A_2$, we need to find all points $(x, y)$ that are in both $A_1$ and $A_2$, which amounts to finding all $x\in\R$ with $x>0$ such that $$ \frac{1}{x} = \frac{1}{x^2} \;\Longrightarrow\; x^2 = x \;\Longrightarrow\; x = 1. $$ So we can conclude that $(1,1)\in A_1\cap A_2$. Furthermore, this solution is unique, so $A_1\cap A_2 = \{(1, 1)\}$.
For any arbitrary $k\in\N$, we get for $x=1$: $$ \frac{1}{1^k} = 1 $$ so $(1,1)\in A_k$. We can therefore conclude that $$ \bigcap_{\alpha\geq 1} A_\alpha = \{(1, 1)\}. $$
Problem 9
Let $y = f(x) = \langle x\rangle$ for all real $x$, where $\langle x\rangle$ is the fractional part of $x$, i.e $x = 3.635$ means $\langle x\rangle = 0.635$ and $x = -2.6$ means $\langle x\rangle = 0.6$.Claim: Every closed interval of length 1 has the same image under $f$.
Proof.
Suppose $a$ and $b$ are two arbitrary, real numbers. We will consider the closed intervals $D_1 = [a, a+1]$ and $D_2 = [b, b+1]$. We want to prove that $f(D_1) = f(D_2)$, i.e. show that these sets are included in each other
$\subset)$. Assume $x\in f(D_1)$. Since this is the fractional part, $x = 0.d_1d_2d_3\ldots$ where $d_i$ is some integer between 1 and 9 for each $i$. Since $D_2$ is an interval of length 1, there will be some $z\in D_2$ such that $z = c.d_1d_2d_3\ldots$, but then $f(z) = 0.d_1d_2d_3\ldots = x\in f(D_2)$ which shows that $f(D_1)\subset f(D_2)$.
$\supset)$. By assuming $x\in f(D_2)$ and using the exact same argument as above, we can show that $f(D_2)\subset f(D_1)$.
By inclusion both ways, $f(D_1) = f(D_2)$.
■
The image of $f$ is $[0,1)$. For any integer $p\in\Z$, we will get $f(p) = 0$ and the rest of the interval is filled with all values that are not integers.
The function $f$ is NOT one-to-one. Counter examples are $1.5$ and $2.5$ that both map to $0.5$ which violates the injective property, so we cannot have a bijection and so $f$ is not one-to-one.
The preimage of $1/4\leq y\leq 3/4$ will be the closed intervals: $$ \ldots, [-1.75, -1.25], [-0.75, -0.25], [0.25, 0.75], [1.25, 1.75], [2.25, 2.75], \ldots $$ Or, more generally: $$ \Big\{[p+0.25, p+0.75]\;\big|\; p\in\Z\Big\}. $$ We can find a partition (a collection of pairwise disjoint subsets of $\R$) by defining the following half-closed intervals: $$ \Big\{[p, p+1)\;\big|\; p\in\Z\Big\}. $$
Problem 10
Given a set $M$ and let $\mathscr{R}$ be the set of all ordered pairs on the form $(a,a)$ with $a\in M$. Let $aRb$ iff $(a,b)\in\mathscr{R}$. Interpreting the relation $R$.Since $(a,b)\in\mathscr{R}$, this means that $b = a$, which again means that $aRb$ is $a=b$. The relation is simply equality.
Before going to the next problem. Recall the three properties of an equivalence relation $R$ defined on some set $M$.
- Reflexivity: $aRa$ for every $a\in M$.
- Symmetry: If $aRb$ then $bRa$
- Transitivity: If $aRb$ and $bRc$, then $aRc$
Problem 11
Example of binary relations that do not satisfy all properties.(a). Reflexive and symmetric, but not transitive.
Going out of the realm of mathematics and applying this to family relations. If we define $B$ as being blood relative (common grandparents), then $aBa$ is true for a person $a$. If $aBb$ then $b$ is a cousin or sibling, which implies $bBa$. If $b$ is a cousin of $a$, and $c$ a cousin of $b$, then $aBb$ and $bBc$ holds, but not necessarily $aBc$. So the blood relation $B$ is reflexive and symmetric, but not transitive.
(b). Reflexive, but neither symmetric nor transitive.
Let $M$ be all humans, and define the relation $K$ which means to know someone's name. If we disregard people with amnesia etc. then all people know their own name, so $aKa$ is satisfied. If $aKb$ it is not always the case that $bKa$, so this relation is not symmetric. (For instance if $b$ is a celebrity). It is not transitive, for $aKb$ and $bKc$ does not mean $aKc$. It is not always the case that person $a$ knows everyone $b$ knows. In summary, the $K$ relation is reflexive, but not symmetric and not transitive.
(c). Symmetric, but neither reflexive nor transitive.
Again, let $M$ be all humans and let $R$ mean to be in a romantic relationship. A person $a$ cannot be in a romantic relationship with himself/herself, so $aRa$ is not possible. If $aRb$ then $bRa$ (disregarding some of the complexity of the human psyche here), which means the relation is symmetric. If $aRb$ and $bRc$ it is not always the case that $aRc$, such as in the case when $b$ is unfaithful to $a$. So transitivity is not satisfied.
(d). Transitive, but neither reflexive nor symmetric.
This is achieved with the strictly greater than operator. For some $a,b,c\in\R$, then it is not reflexive since $a < a$ is not true. And if $a < b$, then $b > a$ cannot be true. But if $a < b$ and $b < c$, then $a < c$ holds. The $<$ operator is not reflexive, not symmetric, but it is transitive.