Chapter 4 - Conditional Probability

4.2 Continuous Conditional Probability

Main:	Index
Previous:	4.1 Discrete Conditional Probability
Next:	5.1 Important Distributions

Results

If X is a continuous random variable with density function f(x), and if E is an event with positive probability, we define a conditional density function by the formula $$ f(x|E) = \left\{ \begin{matrix} f(x)/P(E) & x\in E, \\ 0 & x\not\in E. \end{matrix} \right. $$ Then, for any event F, we have $$ P(F|E) = \int_F f(x|E)dx. $$ Alternative expression: $$ P(F|E) = \int_F f(x|E)dx = \int_{E\cap F} \frac{f(x)}{P(E)} dx = \frac{P(E\cap F)}{P(E)}. $$




Just as in the discrete case, independence is defined in the same way. The events E and F are independent if, $$ P(E|F) = P(E), \qquad P(E\cap F) = P(E)P(F). $$




Let X₁, X₂, ..., X_n be continuous random variables associated with an experiment, and let X = (X₁, X₂, ..., X_n). Then the joint cumulative distribution function of X is defined by, $$ F(x_1, x_2, \ldots, x_n) = P(X_1\leq x_1, X_2\leq x_2, \ldots, X_n\leq x_n). $$ The joint density function of X satisfies the following equation: $$ F(x_1, x_2, \ldots, x_n) = \int_{-\infty}^{x_1}\int_{-\infty}^{x_2} \cdots\int_{-\infty}^{x_n} f(t_1, t_2, \ldots, t_n)dt_n dt_{n-1}\ldots dt_1. $$




Let X₁, X₂, ..., X_n be continuous random variables with cumulative distribution functions F₁(x), F₂(x), ..., F_n(x). Then these variables are mutually independent if $$ F(x_1, x_2, \ldots, x_n) = F_1(x_1)F_2(x_2)\cdots F_n(x_n) $$ for any choice of x_i. Thus, if X₁, X₂, ..., X_n are mutually independent, then the joint cumulative distribution function of the random variable X = (X₁, X₂, ..., X_n) is just the product of the individual CDFs. When two variables are mutually independent, we just say that they are independent.




Let X₁, X₂, ..., X_n be continuous random variables with PDFs f₁(x), f₂(x), ..., f_n(x). Then these random variables are mutually independent if and only if $$ f(x_1, x_2, \ldots, x_n) = f_1(x_1)f_2(x_2)\cdots f_n(x_n) $$ for any choice of x_i.




Let X₁, X₂, ..., X_n be mutually independent random variables and let φ₁(x), φ₂(x), ..., φ_n(x) be continuous functions. Then φ₁(X₁), φ₂(X₂), ..., φ_1n(X_n) are mutually independent.




A sequence X₁, X₂, ..., X_n of random variables X_i that are mutually independent and have the same density is called an independent trials process.

Exercise 1

Pick a point x at random (with uniform density) in the interval [0, 1]. Find the probability that x > 1/2, given that

(a) x > 1/4.
(b) x < 3/4.
(c) |x − 1/2| < 1/4.
(d) x² − x + 2/9 < 0.

Answer
We are using the uniform distribution on [0, 1], so f(x) = 1. In the exercises we define the event x > 1/2 as F, and the given event as E.

(a)
Here E = {x | x > 1/4}. We calculate the probability of E: $$ P(E) = \int_E f(t)dt = \int_{1/4}^1 1 dt = \Big[t\Big]_{1/4}^1 = 1 - 1/4 = 3/4. $$ So, since F ⊂ E; $$ P(F|E) = \int_F f(t)/P(E) dt = \int_{1/2}^1 \frac{4}{3}dt = \Big[\frac{4t}{3}\Big]_{1/2}^1 = \frac{4}{3}\Big[t\Big]_{1/2}^1 = \frac{4}{3}[1 - 1/2] = \frac{4}{3}\cdot \frac{1}{2} = \frac{4}{6} = \frac{2}{3}. $$ (We are scaling up the probability, since we are restricting the condition to a smaller area. Makes sense!)

(b)
E = {x | x < 3/4}. We calculate the probability of E: $$ P(E) = \int_E f(t)dt = \int_{0}^{3/4} 1 dt = \Big[t\Big]_{0}^{3/4} = 3/4 - 0 = 3/4. $$ In this case, F = {x | x > 1/2}, so E ∩ F = {x | x ∊ [1/2, 3/4]}. $$ P(F|E) = \int_F f(t)/P(E) dt = \frac{4}{3}\int_{1/2}^{3/4} 1dt = \frac{4}{3}\Big[t\Big]_{1/2}^{3/4} = \frac{4}{3}[3/4 - 2/4] = \frac{4}{3}\cdot \frac{1}{4} = \frac{1}{3}. $$

(c)
Reformulating:
|x − 1/2| < 1/4 ==> −1/4 < x − 1/2 < 1/4 ==> 1/4 < x < 3/4. So in this case, E = {x | x ∊ [1/4, 3/4]}. Calculating the probability of E: $$ P(E) = \int_E f(t)dt = \int_{1/4}^{3/4} 1 dt = \Big[t\Big]_{1/4}^{3/4} = 3/4 - 1/4 = 1/2. $$ F = {x | x > 1/2}, so E ∩ F = {x | x ∊ [2/4, 3/4]}. $$ P(F|E) = \int_F f(t)/P(E) dt = 2\int_{2/4}^{3/4} 1dt = 2\Big[t\Big]_{2/4}^{3/4} = 2[3/4 - 2/4] = 2\cdot \frac{1}{4} = \frac{1}{2}. $$

(d)
Reformulating.
x² − x + 2/9 < 0 ==> (x - 1/3)(x - 2/3) < 0. Zero points when x=1/3 or x=2/3. When inserting x=0 or x=1 it is positive, but it is negative for values between 1/3 and 2/3.
Hence, E = {x | x ∊ [1/3, 2/3]}. Calculating the probability of E: $$ P(E) = \int_E f(t)dt = \int_{1/3}^{2/3} 1 dt = \Big[t\Big]_{1/3}^{2/3} = 2/3 - 1/3 = 1/3. $$ F = {x | x > 1/2}, so E ∩ F = {x | x ∊ [1/2, 2/3]}, or E ∩ F = {x | x ∊ [3/6, 4/6]}. $$ P(F|E) = \int_F f(t)/P(E) dt = 3\int_{3/6}^{4/6} 1dt = 3\Big[t\Big]_{3/6}^{4/6} = 3[4/6 - 3/6] = 3\cdot \frac{1}{6} = \frac{1}{2}. $$

Exercise 2

A radioactive material emits α-particles at a rate described by the density function (and distribution function as shown in Example 4.20) $$ f(t) = 0.1 e^{−0.1t} \;\;\Longrightarrow\;\; F(t) = 1 - e^{-0.1t}. $$ Find the probability that a particle is emitted in the first 10 seconds, given that

(a) no particle is emitted in the first second.
(b) no particle is emitted in the first 5 seconds.
(c) a particle is emitted in the first 3 seconds.
(d) a particle is emitted in the first 20 seconds.

Answer
Let E be the event that a particle is emitted within the first 10 seconds. G is the event specified in each question.

(a)
Finding the probability that a particle is emitted in the first second: F(1) = 1 - exp(-0.1) ≈ 0.09516. The event G is that this does not happen, so P(G) = 1 - F(1) = 0.9048.

We must find the intersetion E ∩ G = {emitted within 10 seconds AND not emitted in first second}, so this becomes the event that a particle is emitted between 1 and 10 seconds. $$ P(E|G) = \frac{P(E\cap G)}{P(G)} = \frac{F(10) - F(1)}{0.9048} = \frac{0.5369}{0.9048} = 0.5934. $$ By the memoryless property, we could also just calculate: $$ F(9) = 1 - e^{-0.9} = 0.5934. $$

(b)
Similar to (a). The probability there is a particle is emitted within the first five seconds: F(5) = 1 - exp(-0.5) ≈ 0.3934. The event G is that this does not happen, so P(G) = 1 - F(5) = 0.6065.

E ∩ G = {emission between 5 and 10 seconds}, so P(E ∩ G) = F(10) - F(5). $$ P(E|G) = \frac{P(E\cap G)}{P(G)} = \frac{F(10) - F(5)}{0.6065} = \frac{0.2386}{0.6065} = 0.3934. $$ By the memoryless property, we could also just calculate: $$ F(5) = 1 - e^{-0.5} = 0.3934. $$

(c)
E ∩ G = {emitted within 10 seconds AND emitted within 3 seconds} = {emitted within 3 seconds} = G, since G ⊂ E. In this case we get: $$ P(E|G) = \frac{P(E\cap G)}{P(G)} = \frac{P(G)}{P(G)} = 1, $$ which makes sense, since the event has already happened.

(d)
G: a particle is emitted within the first 20 seconds, so P(G) = F(20) = 1 - exp(-2) = 0.8646. This time, since E ⊂ G, we get E ∩ G = E. Recalling that P(E) = F(10) = 1 - exp(-1) = 0.6321. $$ P(E|G) = \frac{P(E\cap G)}{P(G)} = \frac{P(E)}{P(G)} = \frac{F(10)}{F(20)} = \frac{0.6321}{0.8646} = 0.7310. $$

Exercise 3

The Acme Super light bulb is known to have a useful life described by the density function $$ f(t) = 0.01 e^{−0.01t} \;\;\Longrightarrow\;\; F(t) = 1 - e^{-0.01t}. $$ where t is measured in hours.

(a) Find the failure rate of this bulb (see Exercise 2.2.6).
(b) Find the reliability of this bulb after 20 hours.
(c) Given that it lasts 20 hours, find the probability that the bulb lasts another 20 hours.
(d) Find the probability that the bulb burns out in the forty-first hour, given that it lasts 40 hours.

Answer

(a)
The failure rate is simply the λ parameter, which in this case is 0.01.

(b)
Following the methods in exercise 2.2.6, we get that the reliability after 20 hours is: $$ P(t > T) = e^{-0.2} = 0.8187. $$

(c)
Let F be the event that the bulb lasts more than 40 hours: F = {t > 40}, and let M be the event that the bulb lasts more than 20 hours: M = {t > 20}. We want to find P(F|M). Note that since F is a subset of M, we get: F ∩ M = {t > 40}∩{t > 20} = {t > 40} = F. To find the probabilities:

P(F) = P(t > 40) = 1 - P(t ≤ 40) = 1 - F(40).
P(M) = P(t > 20) = 1 - P(t ≤ 20) = 1 - F(20).

Calculating the probability: $$ P(F|M) = \frac{P(F\cap M)}{P(M)} = \frac{P(F)}{P(M)} = \frac{1 - F(40)}{1 - F(20)} = \frac{0.67032}{0.8187} = 0.81873 $$ By the memoryless property, this could have been calculated as: $$ 1 - F(20) = 0.81873 $$

(d)
This is similar to (c). Call the events F and M again. M is the event that P(t > 40), and F is the event that P(t ≤ 41). Finding the probabilities:

P(F) = P(t ≤ 41) = F(41).
P(M) = P(t > 40) = 1 - P(t ≤ 40) = 1 - F(40).

Now, to find the intersection:
F ∩ M = {t ≤ 41}∩{t > 40} = {40 < t ≤ 41}. So, P(F ∩ M) = F(41) - F(40). $$ P(F|M) = \frac{P(F\cap M)}{P(M)} = \frac{F(41) - F(40)}{1 - F(40)} = \frac{0.006669796}{0.67032} = 0.009950167 $$ By the memoryless property, this could have een calculated as: $$ F(1) = 0.009950166 $$

Exercise 4

Suppose you toss a dart at a circular target of radius 10 inches. Given that the dart lands in the upper half of the target, find the probability that

(a) it lands in the right half of the target.
(b) its distance from the center is less than 5 inches.
(c) its distance from the center is greater than 5 inches.
(d) it lands within 5 inches of the point (0, 5).

Answer
In all that follows, we will define the event U as the dart landing in the upper half of the target.
U = {(x,y) | y ≥ 0}.
Calculating the probability, using a geometric argument. The area is half the dart area, specifically the top half, so P(U) = 1/2.

(a)
The event E is the dart landing in the right hand side of the target. So, the area F ∩ M becomes the top right quadrant of the map, and P(F ∩ M) = 1/4. $$ P(E|U) = \frac{P(E\cap U)}{P(U)} = \frac{1/4}{1/2} = 1/2. $$ Sketch of area.


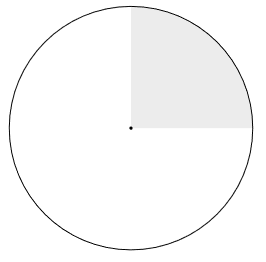
(b)
The event E is the dart landing within 5 inches of the center, sp Area(E) = π(5)² = 25π, and then the probability is P(E) = 25π/100π = 1/4. When finding E ∩ U it will be half this circle, so Area(E ∩ U) = (25/2)π, and so P(E ∩ U) = (25π/2)/(100π) = 25/100 = 5/40 = 1/8. $$ P(E|U) = \frac{P(E\cap U)}{P(U)} = \frac{1/8}{1/2} = 1/4. $$ Sketch of area.


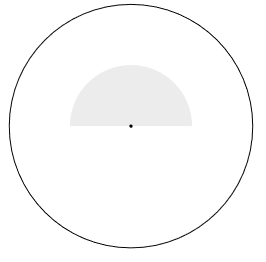
(c)
Now the area is at least 5 inches from the center, so this is the complement to the area in (b), so Area(E) = 100π - 25π = 75π. Again, when restricting this to the upper half, this area is halfed, so Area(E ∩ U) = 75π/2, and so P(E ∩ U) = (75π/2)/(100π) = 75/200 = 15/40 = 3/8. $$ P(E|U) = \frac{P(E\cap U)}{P(U)} = \frac{3/8}{1/2} = 3/4. $$ Sketch of area.


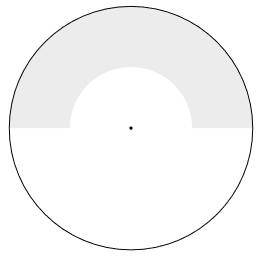
(d)
The region of E is the circle with center in (0, 5) and with radius 5. Area(E) = 25π. Since E ⊂ U, Area(E ∩ U) = Area(E) = 25π. So P(E ∩ U) = P(E) = 25π/100π = 1/4. $$ P(E|U) = \frac{P(E\cap U)}{P(U)} = \frac{1/4}{1/2} = 1/2. $$ Sketch of area.

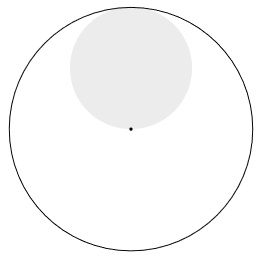
Exercise 5

Suppose you choose two numbers x and y, independently at random from the interval [0, 1]. Given that their sum lies in the interval [0, 1], find the probability that

(a) |x − y| < 1.
(b) xy < 1/2.
(c) max{x, y} < 1/2.
(d) x 2 + y 2 < 1/4.
(e) x > y.

Answer
This exercise is quite similar to exercise 2.2.8.

For x,y ∊ [0, 1], we have the event S = {x + y ∊ [0, 1]}. A few points:
If x = 0, then y = 1.
If x = 1, then y = 0.
If x = 1/2, then y = 1/2.
Together these form the boundary line, and every point below this line is included in the set S. The set S takes up half the unit square, which we use to visualize the area. P(S) = 1/2.

Sketch image.


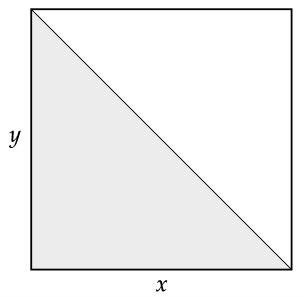
(a)
We found the area for |B-C| < 1/2 in 2.2.8(d). Now we have |x-y| < 1 which will take up the entire unit square. If we call this W = {x,y ∊ [0, 1] : |x-y| < 1}, then P(W) = 1.

Since S ⊂ W, then S ∩ W = S. So, we can calculate the area: $$ P(W|S) = \frac{P(W\cap S)}{P(S)} = \frac{P(S)}{P(S)} = 1. $$ Sketch image.


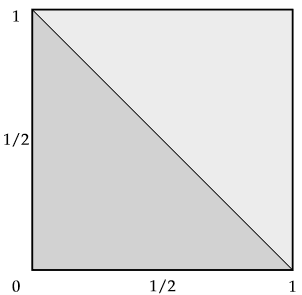
(b)
Define the event Q = {x,y ∊ [0, 1] | xy < 1/2}. We found this area in 2.2.8(c) and as we found, it forms an area constrained by a curve in the top right. We can see that S ⊂ Q, so S ∩ Q = S. $$ P(Q|S) = \frac{P(Q\cap S)}{P(S)} = \frac{P(S)}{P(S)} = 1. $$ Sketch image.


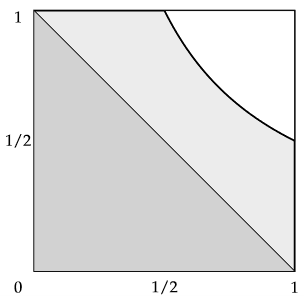
(c)
As found in 2.2.8, the area R = {x,y ∊ [0, 1] | max(x,y) < 1/2} is the lower quarter area of the unit square. So, P(R) = 1/4. Also, we see that R ⊂ S, so R ∩ S = R, so P(R ∩ S) = 1/4. $$ P(R|S) = \frac{P(R\cap S)}{P(S)} = \frac{P(R)}{P(S)} = \frac{1/4}{1/2} = 1/2. $$ Sketch image.


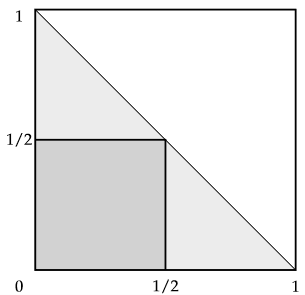
(d)
This is a new area, but it is a quarter of the circle centered at (0,0) with a radius of 1/2. Let us define the area as C = {x,y ∊ [0, 1] | x² + y² < 1/4}. The probability of C is one fourth the area of the circle. Denote the area function as A(). $$ P(C) = \frac{A(C)}{4} = \frac{\pi(1/2)^2}{4} = \frac{\pi}{16}. $$ Since C ⊂ S, so C ∩ S = C, so P(C ∩ S) = π/16. $$ P(C|S) = \frac{P(C\cap S)}{P(S)} = \frac{P(C)}{P(S)} = \frac{\pi/16}{1/2} = \pi/8. $$ Sketch image.


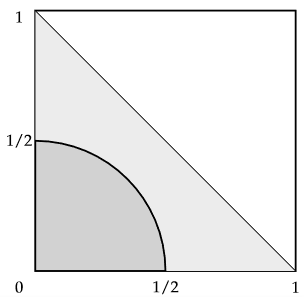
(e)
Define L = {x,y ∊ [0, 1] | x > y}. The area where x=y is the diagonal line from (0,0) to (1,1). Everything to the right of this line is the area where x > y. From the sketch image below, we note that P(L ∩ S) = 1/4 as it makes up one fourth of the total area. $$ P(L|S) = \frac{P(L\cap S)}{P(S)} = \frac{1/4}{1/2} = 1/2. $$ Sketch image.

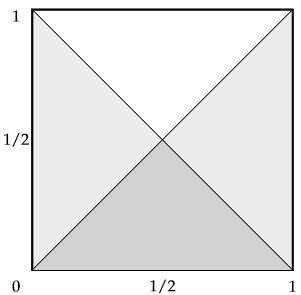
Exercise 6

Find the conditional density functions for the following experiments.

(a) A number x is chosen at random in the interval [0, 1], given that x > 1/4.
(b) A number t is chosen at random in the interval [0, ∞) with exponential density e^−t , given that 1 < t < 10.
(c) A dart is thrown at a circular target of radius 10 inches, given that it falls in the upper half of the target.
(d) Two numbers x and y are chosen at random in the interval [0, 1], given that x > y.

Answer

(a)
Assuming that this is the uniform distribution, so f(x) = 1 on the interval [0, 1]. The distribution will be conditioned on the set E = {x | x > 1/4}. We calculate the probability: $$ P(E) = \int_E f(x)dx = \int_{1/4}^1 1 dx = \Big[x\Big]_{1/4}^1 = 1 - 1/4 = 3/4. $$ So, f(x)/P(E) = 1/(3/4) = 4/3. Using the definition of conditional probability as mentioned on the top. $$ f(x|E) = \left\{ \begin{matrix} 4/3, & x\in E \\ 0, & x\not\in E. \end{matrix} \right. $$ (Probabilities are scaled up since we are restricting it to a smaller area).

(b)
Here, f(t) = e^-t, and the set E = {t | t ∊ (1, 10)}. Calculating P(E). $$ P(E) = \int_E f(t)dt = \int_1^{10} e^{-t}dt = \Big[-e^{-t}\Big]_1^{10} = e^{-1} - e^{-10} \approx 0.3678. $$ Specifying the conditional distribution function. $$ f(t|E) = \left\{ \begin{matrix} \frac{\exp\{-t\}}{0.3678}, & x\in E \\ 0, & x\not\in E. \end{matrix} \right. $$

(c)
As found in exercise 2.2.4, the total area of the dart board is 100π. So, the pdf is f(x,y) = 1/100π. The event E is the top half of the dart board and so P(E) = 1/2, so 1/P(E) = 2. $$ f((x,y)|E) = \left\{ \begin{matrix} \frac{1}{50\pi}, & x\in E \\ 0, & x\not\in E. \end{matrix} \right. $$

(d)
This is part (e) from the previous exercise. Assuming a uniform distribution, so f(x) = 1. When represented in the unit square, we found that E = {x,y ∊ [0,1] | x > y} has a probability of 1/2. So 1/P(E) = 2. $$ f(x|E) = \left\{ \begin{matrix} 2, & x\in E \\ 0, & x\not\in E. \end{matrix} \right. $$

Exercise 7

Let x and y be chosen at random from the interval [0, 1]. Show that the events x > 1/3 and y > 2/3 are independent events.

Answer
First we consider f(x) and f(y) as two separate uniform distributions on [0,1], so f(x) = 1 = f(y). Define the sets A = {x | x > 1/3} and B = {y | y > 2/3}. $$ P(A) = \int_{1/3}^1 1dx = \Big[x\Big]_{1/3}^1 = 1 - 1/3 = 2/3. $$ $$ P(B) = \int_{2/3}^1 1dy = \Big[y\Big]_{2/3}^1 = 1 - 2/3 = 1/3. $$ When multiplying these, we get (2/3)(1/3) = 2/9.

Considering it as a two-dimensional PDF, f(x,y) = 1. \begin{align} P(A\cap B) &= \int_{2/3}^1\int_{1/3}^1 1 dx dy \\&\\ &= \int_{2/3}^1 \Big[x\Big]_{1/3}^1 dy \\&\\ &= \int_{2/3}^1 2/3 dy \\&\\ &= 2/3\Big[y\Big]_{2/3}^1 \\&\\ &= (2/3)(1/3) \\&\\ &= 2/9 \end{align} As we can see, P(A ∩ B) = P(A)P(B), which shows that A and B are independent.

Exercise 8

Let x and y be chosen at random from the interval [0, 1]. Which pairs of the following events are independent?

(a) x > 1/3.
(b) y > 2/3.
(c) x > y.
(d) x + y < 1.

Answer
Define the events as A, B, C and D. Here is a sketch of the areas and their probabilities.


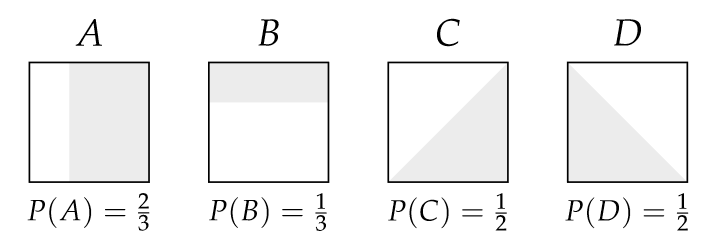
Sketching the intersections of all these sets.


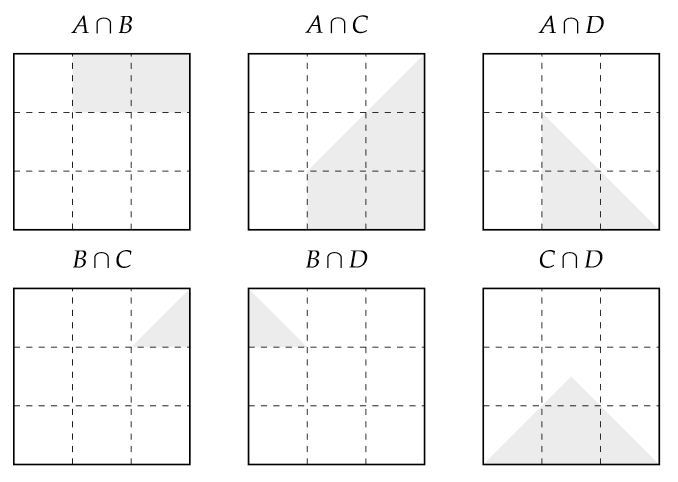
Now we can just compare the probability of the sets with the probability of their intersection. \begin{align} P(A)P(B) = \frac{2}{3}\cdot\frac{1}{3} = \frac{2}{9} &= \frac{2}{9} = P(A\cap B) \\&\\ P(A)P(C) = \frac{2}{3}\cdot\frac{1}{2} = \frac{1}{3} &\not= \frac{4}{9} = P(A\cap C) \\&\\ P(A)P(D) = \frac{2}{3}\cdot\frac{1}{2} = \frac{1}{3} &\not= \frac{2}{9} = P(A\cap D) \\&\\ P(B)P(C) = \frac{1}{3}\cdot\frac{1}{2} = \frac{1}{6} &\not= \frac{1}{18} = P(B\cap C) \\&\\ P(B)P(D) = \frac{1}{3}\cdot\frac{1}{2} = \frac{1}{6} &\not= \frac{1}{18} = P(B\cap D) \\&\\ P(C)P(D) = \frac{1}{2}\cdot\frac{1}{2} = \frac{1}{4} &= \frac{1}{4} = P(C\cap D) \end{align}

The independent sets are A, B and C, D.

Exercise 9

Suppose that X and Y are continuous random variables with density functions f_X(x) and f_Y(y), respectively. Let f(x, y) denote the joint density function of (X, Y). Show that, $$ \int_{-\infty}^{\infty}f(x,y)dy = f_X(x), \qquad \int_{-\infty}^{\infty}f(x,y)dx = f_Y(y). $$

Answer
Showing the first case - the other case is completely analogous. \begin{align} \int_{-\infty}^{\infty}f(x,y)dy &= \int_{-\infty}^{\infty}f_{Y|X}(y|x)f_X(x)dy \\&\\ &= f_X(x)\int_{-\infty}^{\infty}f_{Y|X}(y|x)dy \\&\\ &= f_X(x)\cdot 1 \\&\\ &= f_X(x) \end{align} The $f_X(x)$ is independent of $y$ and can be put outside. The integral becomes 1 by definition of probability distributions.

Exercise 10-14

Skipped...